Задача 1:

«Доказать, что

Какое целое число здесь пропущено?

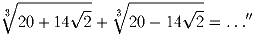
(Жозеф Бертран)

Решение: 4

Задача 2:

Лестница длиной 13 футов наклонно приставлена к стене, нижняя часть ее при этом удалена от стены на 5 футов. Насколько спустится она по стене, если её основание отодвинуть ещё на 7 футов?

(рукопись Мюнхенского собрания)

Решение: 7 футов

Задача 3:

Какое число, будучи прибавлено к девяти, даст свой ушестерённый квадратный корень?

(Абен-Дреат)

Решение: 9

Задача 4:

«Решить в натуральных числах систему: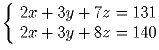.» Сколько всего решений у этой системы?

(Лебег)

Решение: 12 решений

Задача 5:

Число состоит из трех цифр, сумма этих цифр равна 11, цифра единиц вдвое больше цифры сотен. Если прибавить к искомому числу 297, то получается число, написанное теми же цифрами, как у искомого, но в обратном порядке. Какое число имеет эти свойства?

(Луи Пьер Бурдон)

Решение: 326

Задача 6:

Какое число следует прибавить к каждому из членов дроби 3/11, чтобы получить дробь, равную 5/9 ?

(Желен)

Решение: 7

Задача 7:

Некто согласился работать с условием получить в конце года одежду и 10 флоринов. Но по истечении 7 месяцев прекратил работу и при расчете получил одежду и 2 флорина. Во сколько ценилась одежда?

(Христоф Рудольф)

Решение:

Задача 8:

«Если число, делённое на 9, даёт в остатке 2, 5 или 8, то куб его, делённый на 9, даёт в остатке ». Что?

(Авиценна)

Решение: 8

Задача 9:

Найти последний член и сумму 20 членов прогрессии: 3, 7, 11, 15,

(Ал-Кархи)

Решение: 820

Задача 10:

Разложить дробь 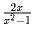на сумму двух дробей вида .

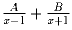(Огюстен Луи Коши)

Решение: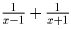

Задача 11:

Трое выиграли некоторую сумму денег. На долю первого пришлась 1/4 этой суммы, на долю второго – 1/7, а на долю третьего – 17 флоринов. Как велик весь выигрыш?

(Адам Ризе)

Решение: 28 флоринов

Задача 12:

Найти число, которое, будучи умножено на 3, а затем разделено на 5, увеличено на 6, после чего из него извлечён квадратный корень, отнята единица и результат возведён в квадрат, даст 4.

(Парамадисвара)

Решение: 5

Задача 13:

Один фонтан наполняет бассейн в 2½ часа, другой – в 3¾ часа. Во сколько времени оба фонтана, действуя вместе, наполнят бассейн?

(Сильвестр Лакруа)

Решение: за 1,5 часа

Задача 14:

Найти число, которое, будучи увеличено двумя третями самого себя и единицей, даёт 10.

(Бега Эддин)

Решение: 5,4