 |
 |
|
| Задачная база >> Соревнования всероссийского уровня >> Уральский турнир юных математиков >> XVII турнир (февраль, 2001) >> Математическая карусель >> Зачётные задачи. Старшая группа | Убрать решения |
|
|
| XVII Уральский (IX кировский) турнир юных математиков. Математическая карусель. Зачётные задачи. Старшая группа |
|
|
«Если диаметр круга единица, то длина нити, охватывающей окружность, выражается целым с дробью: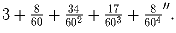 Определить до какого
десятичного знака точно это приближение для π .
Определить до какого
десятичного знака точно это приближение для π .
(Ибн-Эзра Авраам бен-Меир, трактат ``Книга о числе''.)
Решение: Точно до второго десятичного знака Задача 2:Несколько купцов внесли в общее дело 100 раз столько рублей, сколько было купцов. Они отправили в Венецию доверенного, получавшего с каждой сотни рублей число рублей, вдвое большее числа купцов. Спрашивается: сколько было купцов, если доверенный получил 2662 рубля?
(Леонард Эйлер)
Решение: 11 купцов Задача 3:Каким наименьшим числом гирь и какого веса можно отвесить на весах любое целое число фунтов от 1 до 40 при условии, что при взвешивании гири можно класть на обе чаши весов?
(Баше де Мезирак)
Решение: 4 гири – 1, 3, 9 и 27 фунтов Задача 4:Решить уравнение:
13x² = x4 + 2x³ + 2x + 1
(Джироламо Кардано)
Решение: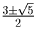 ,
, 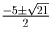 Задача 5:
Задача 5: Стая обезьян забавлялась: квадрат одной восьмой части их резвился в лесу, остальные двенадцать кричали на вершине холмика. Скажи мне: сколько было всего обезьян?
(Бхаскара)
Решение: 16 или 48 обезьян Задача 6:Дан треугольник со сторонами 9, 12, 15. Найти диаметр круга, вписанного в этот треугольник.
(Эпафродит)
Решение: 6 Задача 7:Семь старух отправляются в Рим. У каждой по семи мулов, каждый мул несёт по семи мешков, в каждом мешке по семи хлебов, в каждом хлебе по семи ножей, каждый нож в семи ножнах. Сколько всех предметов?
(Леонардо Фибоначчи)
Решение: 137,256 предметов Задача 8:Эпитафия Диофанту: «Диофант провел шестую часть жизни в детстве, двенадцатую в юности; после седьмой части, проведенной в бездетном супружестве, и ещё 5 лет у него родился сын, проживший в два раза меньше отца. После смерти сына Диофант прожил только 4 года. Скольких лет Диофант умер?»
(Метродор)
Решение: 84 года Задача 9:Найти три числа так, чтобы произведение любой пары их, увеличенное их суммой, равнялось бы соответственно 8, 15, 24.
(Диофант Александрийский)
Решение: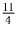 ,
,  ,
, 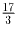 .
Задача 10:
.
Задача 10: «Квадрат хорды, перпендикулярной к диаметру, деленный на учетверённый любой отрезок диаметра и сложенный с тем же отрезком, равняется ?» Чему?
(Брамагупта)
Решение: диаметру Задача 11:Имеется 9 слитков золота и 11 слитков серебра. Их взвесили (золото – на левую чашу весов, серебро – на правую), и весы остались в равновесии. После того, как слиток золота переложили на правую чашу, а слиток серебра – на левую, левая чаша стала легче на 13 ланов. Каков вес одного слитка золота?
(Китай)
Решение: 35¾ = 35,75 лана. Задача 12:«Разделить сто мер пшеницы между 100 лицами так, чтобы каждый мужчина получил 3, каждая женщина – 2, а каждое дитя – ½ меры. Сколько мужчин, женщин и детей?» Сколько решений имеет эта задача?
(Алкуин)
Решение: 7 решений Задача 13:«Сколько раз пробьют часы в продолжение 12 часов, если они отбивают и получасы?" (Часы – соответствующее число раз, а получасы – по разу).
(Луи Франкер)
Решение: 90 раз Задача 14:Дается радиус (4) вписанного в треугольник круга и отрезки 6 и 8, на которые точка касания делит одну сторону треугольника. Найти две другие стороны.
(Лука де Бурго (Пачиоло))
Решение: 13 и 15 Задача 15:«Найти число, которое при делении на 17, 13 и 10 даёт соответственно остатки 15, 11 и 3.» Найдите такое наименьшее натуральное число.
(Региомонтан (Иоганн Мюллер))
Решение: 1103 Задача 16:«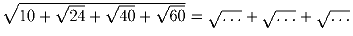 »
Вставьте вместо многоточий натуральные числа.
»
Вставьте вместо многоточий натуральные числа.
(Бхаскара)
Решение: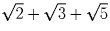 Задача 17:
Задача 17: Некто купил лошадь и спустя некоторое время продал её за 24 пистоля. При этой продаже он теряет столько процентов, сколько стоила ему лошадь. Спрашивается: за какую сумму он ее купил?
(Этьен Безу)
Решение: 40 или 60 пистолей Задача 18:Рота пехоты подходит к берегу реки, но оказывается, что мост сломан, брода нет. У берега два мальчика играют в челноке, но таком маленьком, что в нем может переправиться только один взрослый или двое детей. Спрашивается, как с помощью этого челнока может вся рота переправиться на другой берег?
(Баше де Мезирак)
Решение: Едут дети, один остается, другой обратно, едет солдат, обратно едет лодка с мальчиком, снова едут дети на противоположный берег и т.д. Задача 19:Найти число, которое от умножения на 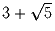 дает единицу.
дает единицу.
(Ал-Кархи)
Решение: Задача 20:
Задача 20: За длину окружности вавилоняне принимали периметр вписанного в эту окружность правильного шестиугольника. Найти приближение для π , которым пользовались вавилоняне.
π = 3
| Задачная база >> Соревнования всероссийского уровня >> Уральский турнир юных математиков >> XVII турнир (февраль, 2001) >> Математическая карусель >> Зачётные задачи. Старшая группа | Убрать решения |