 |
 |
|
| Задачная база >> Соревнования всероссийского уровня >> Уральский турнир юных математиков >> XVII турнир (февраль, 2001) >> Турнир матбоёв >> Математический бой N1 >> Младшая группа, высшая лига | Убрать решения |
|
|
| XVII Уральский (IX кировский) турнир юных математиков. Турнир матбоёв. Математический бой N1. Младшая группа, высшая лига |
|
|
Как разрезать квадрат на 5 частей, из которых можно без пропусков и наложений сложить три попарно неравных квадрата?
Задача 2:
Точки E и F – середины сторон BC и CD квадрата ABCD. Отрезки AE и BF пересекаются в точке K. Что больше – площадь треугольника AKF или площадь четырехугольника KECF?
Задача 3:
Чтобы от театра доехать до цирка, можно сесть на остановке на
автобус 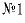 или на автобус
или на автобус 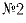 . Они ходят с постоянными интервалами,
причем
автобус
. Они ходят с постоянными интервалами,
причем
автобус 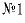 в 2 раза реже, чем
в 2 раза реже, чем 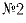 . За последние 20 минут автобус
прошел 16
минут назад, 10 минут назад и 2 минуты назад. Когда будет следующий автобус?
. За последние 20 минут автобус
прошел 16
минут назад, 10 минут назад и 2 минуты назад. Когда будет следующий автобус?
В треугольнике ABC медиана AM равна стороне AB, а угол MAC равен 30. Найдите углы треугольника.
Задача 5:
Решите систему уравнений:
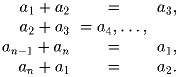
Задача 6:
Сколько существует таких трехзначных чисел n, что n² + 8n – 1 делится на 239?
Задача 7:
В поселке некоторые дома соединены проводами. Соседями называются двое, дома которых связаны проводом. Всегда ли удастся поселить в каждый дом по одному человеку – лжецу или рыцарю (лжецы всегда лгут, рыцари всегда говорят правду) – так, чтобы каждый на вопрос: «Есть ли среди ваших соседей лжецы?» ответил положительно? (Каждый знает про каждого из своих соседей, лжец он или нет).
Задача 8:
Натуральное число удалось разложить на 10 сомножителей, больших единицы, двумя способами так, что ни один из сомножителей первого разложения не совпадает ни с одним из сомножителей второго. Докажите, что это число можно разложить на 14 сомножителей (не обязательно различных), больших единицы.
| Задачная база >> Соревнования всероссийского уровня >> Уральский турнир юных математиков >> XVII турнир (февраль, 2001) >> Турнир матбоёв >> Математический бой N1 >> Младшая группа, высшая лига | Убрать решения |