 |
 |
|
| Задачная база >> Соревнования всероссийского уровня >> Уральский турнир юных математиков >> XVII турнир (февраль, 2001) >> Турнир матбоёв >> Математический бой N2 >> Младшая группа, первая лига | Убрать решения |
|
|
| XVII Уральский (IX кировский) турнир юных математиков. Турнир матбоёв. Математический бой N2. Младшая группа, первая лига |
|
|
Сложите квадрат 8 × 8 из 32 доминошек так, чтобы ни в какой точке не сходились четыре доминошки.
Задача 2:
Найдите наименьшее натуральное число, произведение цифр которого больше 1500.
Задача 3:
Имеется неограниченный запас гирь, каждая весом в целое число граммов. Требуется подобрать такой набор гирь общим весом в n граммов, что любой целочисленный вес, меньший n, можно было единственным образом уравновесить гирями из этого набора (гири одного веса считаются одинаковыми). Класть на одну и ту же чашку гири и груз не разрешается. Простейший способ – взять для этого много гирек весом в 1 грамм. Такой способ мы будем называть тривиальным. Докажите, что для n = 6 нетривиального подбора гирь не существует.
Задача 4:
Каждый ученик класса занимается в двух кружках, и для каждых трех учеников есть кружок, в который они ходят вместе. Докажите, что имеется кружок, в котором занимаются все ученики.
Задача 5:
В круге какого наименьшего диаметра могут найтись четыре точки A, B, C, D такие, что AB = 3, BC = 2, CD = 4, DA = 5?
Задача 6:
Пусть a, b, c и d – такие числа, что ab = 1 и ac + bd = 2. Докажите, что cd ≤ 1.
Задача 7:
Докажите, что при любых натуральных a и b число 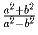 не является целым.
не является целым.
Задача 8:
Сумма 100 целых чисел равна нулю. Докажите, что из них можно по крайней мере 99 способами выбрать два числа, сумма которых неотрицательна.
| Задачная база >> Соревнования всероссийского уровня >> Уральский турнир юных математиков >> XVII турнир (февраль, 2001) >> Турнир матбоёв >> Математический бой N2 >> Младшая группа, первая лига | Убрать решения |