 |
 |
|
| Задачная база >> Соревнования всероссийского уровня >> Уральский турнир юных математиков >> XVII турнир (февраль, 2001) >> Турнир матбоёв >> Математический бой N2 >> Старшая группа, высшая лига | Убрать решения |
|
|
| XVII Уральский (IX кировский) турнир юных математиков. Турнир матбоёв. Математический бой N2. Старшая группа, высшая лига |
|
|
Юра составил из 32 раскрашенных доминошек квадрат 8 × 8 так, что любые две доминошки одного цвета не имеют общих точек. Докажите, что у Юры были доминошки хотя бы четырех цветов.
Задача 2:
На плоскости дано 13 точек, причем из любых пяти четыре лежат на одной окружности. Докажите, что есть окружность, на которой лежат по крайней мере шесть из данных точек.
Задача 3:
Имеется неограниченный запас гирь, каждая весом в целое число граммов. Требуется подобрать такой набор гирь общим весом в n граммов, что любой целочисленный вес, меньший n, можно было единственным образом уравновесить гирями из этого набора (гири одного веса считаются одинаковыми). Класть на одну и ту же чашку гири и груз не разрешается. Простейший способ – взять для этого много гирек весом в 1 грамм. Такой способ мы будем называть тривиальным. Докажите, что если нетривиальный способ подбора гирь существует, то число n + 1 составное.
Задача 4:
D, E и F – основания перпендикуляров, опущенных из внутренней точки M на стороны остроугольного треугольника ABC. Найдите геометрическое место таких точек M, что ∠ DEF = 90.
Задача 5:
Докажите, что среди любых 22 последовательных натуральных чисел найдется число, не делящееся на сумму своих цифр.
Задача 6:
В стране Фалкерсонии некоторые города соединены авиалиниями, причем из города A в город B нельзя попасть, сделав менее десяти пересадок. Докажите, что все авиалинии можно распродать 11 авиакомпаниям таким образом, что любой маршрут из A в B будет проходить по линиям, принадлежащим всем 11 компаниям.
Задача 7:
В остроугольном треугольнике ABC BH – высота. Прямые, симметричные AC относительно AB и BC пересеклись в точке K. Докажите, что угол KBC равен углу ABH.
Задача 8:
Докажите, что при любых натуральных a и b число 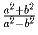 не является целым.
не является целым.
| Задачная база >> Соревнования всероссийского уровня >> Уральский турнир юных математиков >> XVII турнир (февраль, 2001) >> Турнир матбоёв >> Математический бой N2 >> Старшая группа, высшая лига | Убрать решения |