 |
 |
|
| Задачная база >> Соревнования всероссийского уровня >> Уральский турнир юных математиков >> XVII турнир (февраль, 2001) >> Турнир матбоёв >> Математический бой N4 >> Младшая группа, высшая лига | Убрать решения |
|
|
| XVII Уральский (IX кировский) турнир юных математиков. Турнир матбоёв. Математический бой N4. Младшая группа, высшая лига |
|
|
В клетках прямоугольника 5 × 9 стоят 33 фишки. Ход состоит в том, что все фишки одновременно сдвигаются так, чтобы каждая фишка оказалась на клетке, соседней с исходной. При этом запрещается ставить две фишки на одну клетку (в том числе и в начальной позиции). Кроме того, если какая-то фишка передвинулась по горизонтали, то в следующий ход она должна передвигаться по вертикали, и наоборот. Докажите, что по этим правилам невозможно сделать подряд 100 ходов.
Задача 2:
В выпуклом шестиугольнике ABCDEF диагонали AD, BE и CF равны и пересекаются в одной точке. Оказалось, что AB = DE, a BC = EF. Докажите, что CD = FA.
Задача 3:
Найдите все такие числа n, что
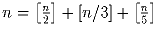 .
[x] – это
наибольшее целое число, не превосходящее числа x.
.
[x] – это
наибольшее целое число, не превосходящее числа x.
Задача 4:
При каких натуральных k, больших 2, но меньших 50, существует число, которое является суммой k идущих подряд натуральных чисел, но не является суммой m идущих подряд натуральных чисел при любом m от 2 до k – 1?
Задача 6:
В треугольнике ABC ∠ B = 120. BL – биссектриса этого треугольника. K и M – основания перпендикуляров, опущенных из точки L на стороны AB и AC соответственно. Докажите, что 2KM < AC.
Задача 7:
В группе из 100 людей среди любых троих есть человек, знающих обоих других. Докажите, что из этой группы можно выбрать компанию из 50 человек, в которой все знакомы друг с другом.
Задача 8:
Можно ли вырезать из клетчатой бумаги 16 прямоугольников так, чтобы из них можно составить любой клетчатый прямоугольник, обе стороны которого не больше 15?
| Задачная база >> Соревнования всероссийского уровня >> Уральский турнир юных математиков >> XVII турнир (февраль, 2001) >> Турнир матбоёв >> Математический бой N4 >> Младшая группа, высшая лига | Убрать решения |