 |
 |
|
| Задачная база >> Соревнования всероссийского уровня >> Зональный этап всероссийской олимпады. >> XXV >> 10 класс | Убрать решения |
|
|
| Зональный этап XXV всероссийской математической олимпиады школьников, 1998/99 учебный год. 10 класс |
|
|
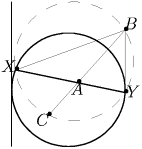
На плоскости даны окружность ω , точка A, лежащая внутри ω , и точка B, отличная от A. Рассматриваются всевозможные треугольники BXY, такие что точки X и Y лежат на ω и хорда XY проходит через точку A. Докажите, что центры окружностей, описанных около треугольников BXY, лежат на одной прямой.
Решение:По теореме о произведении отрезков хорд произведение XA • AY
не зависит от положения хорды XY и равно некоторой постоянной величине
d.
На продолжении отрезка BA за точку A отложим отрезок
AC длины 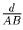 .
.
Тогда AB • AC = XA • AY = d, следовательно точки X, B, Y и C лежат на одной окружности. Это означает, что окружности, описанные около треугольников BXY, проходят через фиксированные точки B и C, следовательно их центры лежат на серединном перпендикуляре к отрезку BC.
 ).
Через каждые три из них проведена плоскость. Докажите, что какие бы
n – 3 точки в пространстве ни взять, найдётся плоскость из проведённых,
не содержащая ни одной из этих n – 3 точек.
).
Через каждые три из них проведена плоскость. Докажите, что какие бы
n – 3 точки в пространстве ни взять, найдётся плоскость из проведённых,
не содержащая ни одной из этих n – 3 точек.
(В.Дольников, С.Игонин)
Решение: Пусть X — произвольное множество из n – 3 точек. Очевидно, что в нашем множестве M есть точка x, не принадлежащая множеству X. Соединим ее прямыми с остальными точками множества M. По условию все эти прямые различны, поэтому их ровно n – 1. Поскольку в множестве X менее n – 1 точки, одна из проведенных прямых не пересекает X. Через эту прямую и оставшиеся (n – 2) точки множества M проведём (n – 2) плоскости. Так как этих плоскостей по-прежнему больше, чем точек во множестве X, одна из них не пересекает X. Эта плоскость и является искомой.Задача 4:
Задача 5: Существуют ли 10 различных целых чисел таких, что все суммы, составленные из 9 из них — точные квадраты?
(Р.Садыков, Е.Черепанов)
Решение:Ответ: Да.
Обозначим искомые числа и их сумму соответственно через x1, … ,x10 и S. Тогда

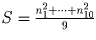 .
Пусть nk = 3k (k = 1, … ,10). Тогда сумма квадратов делится на 9.
Ясно, что числа
.
Пусть nk = 3k (k = 1, … ,10). Тогда сумма квадратов делится на 9.
Ясно, что числа  удовлетворяют требованиям задачи.
Задача 6:
В треугольник ABC вписана окружность, касающаяся
сторон AB, AC и BC в точках C1, B1 и A1 соответственно.
Пусть K —
точка на окружности, диаметрально противоположная точке C1, D — точка
пересечения прямых B1C1 и A1K. Докажите, что CD = CB1.
удовлетворяют требованиям задачи.
Задача 6:
В треугольник ABC вписана окружность, касающаяся
сторон AB, AC и BC в точках C1, B1 и A1 соответственно.
Пусть K —
точка на окружности, диаметрально противоположная точке C1, D — точка
пересечения прямых B1C1 и A1K. Докажите, что CD = CB1.
(М.Евдокимов)
Решение: Заметим, что CA1 = CB1 (как касательные, проведенные к вписанной окружности из одной точки). Пусть окружность с центром в точке C и радиуса CA1 = CB1 пересекает прямую A1K в точке D1. Мы должны доказать, что точки D и D1 совпадают, т.е. что точки D1, B1 и C1 лежат на одной прямой.Прямая KA1 перпендикулярна A1C1 и, следовательно, параллельна
биссектрисе BO. Поэтому 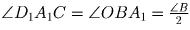 . Угол C при вершине равнобедренного треугольника
A1CD1 равен 180 – 2 • ∠ OBA1 = ∠ A + ∠ C,
следовательно, ∠ B1CD1 = ∠ A.
. Угол C при вершине равнобедренного треугольника
A1CD1 равен 180 – 2 • ∠ OBA1 = ∠ A + ∠ C,
следовательно, ∠ B1CD1 = ∠ A.
В равнобедренных треугольниках D1CB1 и B1AC1 углы при вершинах равны. Поэтому равны и углы при основаниях: ∠ D1B1C = ∠ C1B1A. Это и значит, что точки D1, B1, C1 лежат на одной прямой.
Задача 7: Каждый голосующий на выборах вносит в избирательный бюллетень фамилии n кандидатов. На избирательном участке находится n + 1 урна. После выборов выяснилось, что в каждой урне лежит по крайней мере один бюллетень и при всяком выборе (n + 1)-го бюллетеня по одному из каждой урны найдётся кандидат, фамилия которого встречается в каждом из выбранных бюллетеней. Докажите, что по крайней мере в одной урне все бюллетени содержат фамилию одного и того же кандидата.(В.Дольников)
Решение:Предположим, что утверждение задачи не выполнено. Это означает, что какие бы урну и кандидата ни взять, во взятой урне найдется бюллетень, не содержащий фамилии взятого кандидата.
Выберем произвольный бюллетень из произвольной урны и занумеруем кандидатов, фамилии которых встречаются в этом бюллетене, числами от 1 до n. Этими же числами занумеруем n оставшихся урн. Тогда в k-й урне (k = 1, … ,n) найдётся бюллетень, не содержащий фамилии k-го кандидата. Набор этих бюллетеней вместе с бюллетенем, взятым вначале, противоречит условию задачи.
Задача 8: Некоторые натуральные числа отмечены. Известно, что на каждом отрезке числовой прямой длины 1999 есть отмеченное число. Докажите, что найдётся пара отмеченных чисел, одно из которых делится на другое.
(С.Берлов)
Решение: Рассмотрим отрезки натурального ряда длины 1999. Все они отличаются сдвигом. Назовём точки, или позиции, на двух таких отрезках соответствующими, если они совмещаются при сдвиге одного отрезка на другой.Предположим, что условие задачи не выполняется, т.е. ни одно из отмеченных чисел не делится на другое. Рассмотрим первый отрезок. По условию задачи, в нём есть отмеченное число, скажем x1.
Теперь сдвигаем отрезок на x1. На позиции, соответствующей числу x1, не может стоять отмеченное число, а вместе с тем — есть какое-то другое отмеченное число x2. Теперь сдвинем новый отрезок на x1 • x2. Тогда на позициях, соответствующих отмеченным числам x1 и x2 не могут стоять отмеченные числа, а вместе с тем стоит отмеченное число x3.
Теперь будем сдвигать новый отрезок на x1 • x2 • x3 и найдём новое число x4. На шаге с номером t мы осуществляем сдвиг на x1 • … • xt и получаем отрезок с t запретами.
На шаге с номером 1999 мы получим, что все позиции запрещены, что противоречит условию.
| Задачная база >> Соревнования всероссийского уровня >> Зональный этап всероссийской олимпады. >> XXV >> 10 класс | Убрать решения |