Задача 1: Отец с двумя сыновьями отправились навестить бабушку, которая живёт в 33 км от города. У отца есть мотороллер, скорость которого 25 км/ч, а с пассажиром — 20 км/ч (двух пассажиров на мотороллере перевозить нельзя). Каждый из братьев идёт по дороге со скоростью 5 км/ч. Как им надо действовать, чтобы через три часа всей компанией оказаться у бабушки?

(А.Шаповалов)

Решение: Представляется разумным действовать так. Сначала отец довозит одного из сыновей до места, с которого сын к исходу третьего часа доберется до бабушки, потом возвращается за вторым сыном, и они вместе едут к бабушке. Пусть расстояние до места, где отец должен высадить первого сына, равно x км. Тогда первому сыну до бабушки останется идти 33 – x км, откуда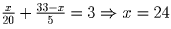 . Эти 24 км отец с сыном проедут за 1,2 часа. Второй сын за это время пройдет 6 км. Затем они с отцом начнут сближаться со скоростью 25 + 5 = 30 км/ч и встретятся через 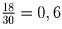 часа в точке, отстоящей от места старта на 5*1,8 = 9 км. Оставшиеся до дома бабушки 24 км они проедут на мотороллере за 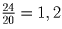 часа. Одновременно с ними там же окажется и первый сын.

Задача 2: К натуральному числу A приписали справа три цифры. Получившееся число оказалось равным сумме всех натуральных чисел от 1 до A. Найдите A.

(И.Акулич)

Решение:

Ответ: 1999. Пусть приписанные цифры образуют число B, 0 ≤ B ≤ 999. Тогда получившееся число равно, с одной стороны, 1000A + B, а с другой — 1 + 2 +  …  + A = ½A(A + 1). Равенство 1000A + B = ½A(A + 1) преобразуется к виду A(A – 1999) = 2B. Понятно, что число A удовлетворяет условию задачи тогда и только тогда, когда 0 ≤ A(A – 1999) ≤ 1998. Поскольку левое неравенство здесь возможно только при A ≥ 1999, а правое — при A < 2000, то единственным решением задачи является A = 1999.

Задача 3: На сторонах BC, CA, AB треугольника ABC выбраны соответственно точки A₁, B₁, C₁ так, что медианы A₁A₂, B₁B₂, C₁C₂ треугольника A₁B₁C₁ соответственно параллельны прямым AB, BC, CA. Определите, в каком отношении точки A₁, B₁, C₁ делят стороны треугольника ABC.

(А.Шаповалов)

Решение: Пусть M — точка пересечения медиан  ∆ A₁B₁C₁ и A₃, B₃, C₃ — точки, в которых продолжения медиан пересекают стороны  ∆ ABC (см. рис). Из условия следует, что MC₃CB₁ — параллелограмм, поэтому MC₃ = CB₁.

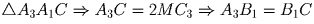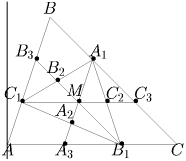
Далее, прямая C₁C₃ проходит через середину отрезка A₁B₁ и параллельна AC, поэтому MC₃ — средняя линия . Но A₂A₃ — средняя линия 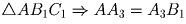, значит, AA₃ = A₃B₁ = B₁C и точка B₁ делит сторону AC в отношении 2:1, считая от вершины A. Аналогично, CA₁:A₁B = BC₁:C₁A = 2:1.

Задача 4: Имеется 40 газовых баллонов, значения давления газа в которых нам неизвестны и могут быть различны . Разрешается соединять любые баллоны друг с другом в количестве, не превосходящем заданного натурального числа k, а затем разъединять их; при этом давление газа в соединяемых баллонах устанавливается равным среднему арифметическому давлений в них до соединения. При каком наименьшем k существует способ уравнивания давлений во всех 40 баллонах независимо от первоначального распределения давлений в баллонах?

(И.Акулич)

Решение:

Ответ: 5. При k = 5 годится следующий способ уравнивания давлений. Разделив баллоны на 8 групп по 5 баллонов, уравняем давления в баллонах каждой из этих групп. Затем образуем 5 новых групп так, чтобы каждая из них состояла из 8 баллонов, входивших ранее в разные группы. Равенства давлений в баллонах каждой из новых групп (а значит, и во всех 40 баллонах) достигнем, соединив сначала баллоны по четыре, а затем — по два, беря в каждую пару баллоны из разных четвёрок.

Покажем, что при k ≤ 4 нужного способа не существует.

Пусть значение давления в одном из баллонов равно 2, а в каждом из остальных — 1; тогда после уравнивания значение давления в каждом баллоне должно оказаться равным .

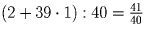Но после каждого соединения все значения будут выражаться несократимыми дробями, знаменатели которых не делятся на 5. В самом деле, если перед каким-либо соединением ни один из знаменателей на 5 не делился, то и знаменатель среднего арифметического соответствующих двух, трёх или четырёх дробей, являясь удвоенным, утроенным или учетверённым наименьшим общим кратным их знаменателей, не может оказаться кратным 5. А так как 40 кратно 5, то уравнять давление при указанных первоначальных их значениях мы не сможем.

Задача 5: Докажите, что из чисел от 1 до 15 нельзя выбрать два числа, произведение которых равно сумме остальных тринадцати.

(Н.Агаханов)

Решение: Пусть такое разбиение возможно и в A вошли числа x и y, x < y. Тогда сумма чисел в B равна 1 + 2 +  …  + 15 – x – y = 120 – x – y, т.е. xy = 120 – x – y. Переписав это равенство в виде (x + 1)(y + 1) = 121, получаем, что либо x + 1 = 1, y + 1 = 121, либо x + 1 = y + 1 = 11, что невозможно.

Задача 6: Дан треугольник ABC. Точка A₁ симметрична вершине A относительно прямой BC, а точка C₁ симметрична вершине C относительно прямой AB. Докажите, что если точки A₁, B и C₁ лежат на одной прямой и C₁B = 2A₁B, то угол CA₁B — прямой.

(Н.Агаханов)

Решение: По условию BC — серединный перпендикуляр к отрезку AA₁, т.е. AB = BA₁ и  ∠ A₁BC =  ∠ ABC. Аналогично, C₁B = BC и  ∠ C₁BA =  ∠ ABC. Итак, 3 ∠ ABC = 180, т.е.  ∠ ABC = 60. Рассмотрим  ∆ CBA₁. В нём  ∠ CBA₁ = 60, CB = C₁B = 2BA₁. Проведём CA₂ ⊥ BA₁. В прямоугольном треугольнике CA₂B  ∠ BCA₂ = 30, поэтому BA₂ = ½BC, т.е. BA₂ = BA₁. Точки A₂ и A₁ совпали, значит,  ∠ CA₁B = 90.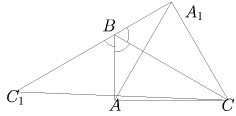

Задача 7: В коробке лежит полный набор костей домино. Два игрока по очереди выбирают из коробки по одной кости и выкладывают их на стол, прикладывая к уже выложенной цепочке с любой из двух сторон по правилам домино. Проигрывает тот, кто не может сделать очередной ход. Кто выиграет при правильной игре?

(Д.Храмцов)

Решение:

Ответ: выигрывает первый игрок.

Опишем выигрышную стратегию I игрока. Вначале он выкладывает на стол 0:0, II отвечает 0:a, тогда I выкладывает кость a:a. Теперь II делает ход либо 0:n, либо a:n. В первом случае I выкладывает кость n:a, во втором — n:0. Тогда после хода I игрока на концах цепочки будут 0 или a. Это же произойдёт после того, как на ход II игрока 0:m (a:m) I ответит m:a (m:0). Кости вида 0:n и a:n (n ≠ 0,a) разбиваются на пары, поэтому последний ход останется за первым игроком.

Задача 8: Из 54 одинаковых единичных картонных квадратов сделали незамкнутую цепочку, соединив их шарнирно вершинами. Любой квадрат (кроме крайних) соединён с соседями двумя противоположными вершинами. Можно ли этой цепочкой квадратов полностью закрыть поверхность куба 3 × 3 × 3?

(А.Шаповалов)

Решение:

Ответ: нельзя.

Предположим противное: закрыть удалось. Тогда, очевидно, каждая грань будет покрыта 9 единичными квадратами. Проведём в каждом квадрате цепочки по диагонали из вершины с шарниром. Получится ломаная из диагоналей на поверхности куба (возможно, пересекающая себя в вершинах звеньев).

Заметим, что из всех ее вершин, кроме, может быть, первой и последней, выходит чётное число ее звеньев (2 или 4). Теперь раскрасим вершины квадратов 1 × 1 в черный и белый цвета в шахматном порядке так, чтобы один из концов ломаной был черным (нетрудно убедиться, что это возможно). Идя по ломаной, видим, что любое ее звено соединяет две черные вершины. Поскольку наша ломаная проходит через все квадраты, она состоит в точности из всех их диагоналей, соединяющих две черные вершины.

Но среди чёрных вершин окажутся 4 вершины куба, а из каждой такой вершины выходит 3 диагонали в другие черные вершины. Получается, что у нашей ломаной должно быть минимум 4 вершины, из которых выходит нечетное число звеньев. Однако мы уже показали, что таких вершин у нее может быть не больше двух. Противоречие.