 |
 |
|
| Задачная база >> Соревнования всероссийского уровня >> Зональный этап всероссийской олимпады. >> XXVII >> 10 класс | Убрать решения |
|
|
| Зональный этап XXVII всероссийской математической олимпиады школьников, 2000/2001 учебный год. 10 класс |
|
|
(Н.Агаханов)
Решение: Из графика квадратного трехчлена видим, что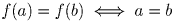 , либо a и b
расположены на числовой оси симметрично относительно точки x0 — абсциссы
вершины параболы, т.е при a + b = 2x0. Но для многоугольника a1 < a2 + … + an,
поэтому a1 + a2 + … + an = 2x0.
Тогда A + B = 2x0, значит, f(A) = f(B).
, либо a и b
расположены на числовой оси симметрично относительно точки x0 — абсциссы
вершины параболы, т.е при a + b = 2x0. Но для многоугольника a1 < a2 + … + an,
поэтому a1 + a2 + … + an = 2x0.
Тогда A + B = 2x0, значит, f(A) = f(B).Задача 2: В параллелограмме ABCD на диагонали AC отмечена точка K. Окружность s1 проходит через точку K и касается прямых AB и AD (s1 вторично пересекает диагональ AC на отрезке AK). Окружность s2 проходит через точку K и касается прямых CB и CD (s2 вторично пересекает диагональ AC на отрезке KC). Докажите, что при всех положениях точки K на диагонали AC прямые, соединяющие центры окружностей s1 и s2, будут параллельны между собой.
(Т.Емельянова)
Решение: Пусть H — гомотетия с центром в точке K и коэффициентом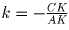 .
Тогда H(A) = C, H(AD) = l1 || AD, так как при гомотетии прямая переходит в
параллельную прямую. Отсюда H(AD) = CD. Следовательно, H(s1) — окружность,
вписанная в угол BCD и проходящая через точку K (H(K) = K). Таким образом,
H(s1) = s2 и, значит, s1 и s2 касаются в точке K.
Прямая, проходящая через точку K перпендикулярно линии центров этих окружностей,
является их общей касательной.
.
Тогда H(A) = C, H(AD) = l1 || AD, так как при гомотетии прямая переходит в
параллельную прямую. Отсюда H(AD) = CD. Следовательно, H(s1) — окружность,
вписанная в угол BCD и проходящая через точку K (H(K) = K). Таким образом,
H(s1) = s2 и, значит, s1 и s2 касаются в точке K.
Прямая, проходящая через точку K перпендикулярно линии центров этих окружностей,
является их общей касательной.Пусть другой точке K′ диагонали AC соответствует другая пара окружностей — s′1 и s′2.
Окружности s1 и s′1 вписаны в угол BAD, следовательно, гомотетичны с центром в точке A, а, значит, их касательные (в точках K и K′ соответственно) параллельны. Отсюда следует, что параллельны и перпендикулярные им линии центров пар окружностей s1, s2 и s′1, s′2.
iv01.102
Задача 3: Опишите все способы покрасить каждое натуральное число в один из трех цветов так, что: если числа a, b и c (не обязательно различные) удовлетворяют условию 2000(a + b) = c, то все они либо одного цвета, либо трех разных цветов.
(Ю.Лифшиц)
Решение: Ответ: Две раскраски: а) все числа одного цвета; б) числа 1, 4, 7, …— цвета A, числа 2, 5, 8, …— цвета B; числа 3, 6, 9, …— цвета C. Положим c = 2000(2d + 2). Тогда из равенства c = 2000((d + 1) + (d + 1)), следует, что числа d + 1 и c одного цвета (a = d + 1, b = d + 1, c = 2000(a + b)).С другой стороны, c = 2000(d + (d + 2)), значит, числа d, d + 2 и d + 1 — одного цвета, или трех разных цветов (a = d, b = d + 2, а d + 1 и c — одного цвета). Значит, любые три последовательных числа либо одного цвета, либо трех разных. Если числа 1, 2, 3 — одного цвета, то рассматривая последовательно тройки 2, 3, 4; 3, 4, 5 и т.д., получаем, что все числа — одного цвета. Если 1 — цвета A, 2 — цвета B, 3 — цвета C, то из тройки 2, 3, 4 получаем, что 4 — цвета A; из тройки 3, 4, 5: что 5 — цвета B, и т.д.
Одноцветная раскраска, очевидно, удовлетворяет условию задачи. Вторая, при которой 3k + 1 — цвета A, 3k + 2 — цвета B, 3k — цвета C, также подходит, так как равенство 2000(a + b) = 2000(3k1 + r1 + 3k2 + r2) = 3M – (r1 + r2) = c = 3k3 + r3 возможно тогда и только тогда, когда r1 + r2 + r3 ≡ 0 (mod %)%3, т.е. числа a, b, c — одного цвета (r1 = r2 = r3), либо трех разных (0 + 1 + 2 = 3 ≡ 0 (mod %)%3).
Задача 4: Проведено три семейства параллельных прямых, по 10 прямых в каждом. Какое наибольшее число треугольников они могут вырезать из плоскости?
(Ю.Лифшиц)
Решение: Ответ: 150. Рассмотрим 100 точек пересечения прямых первого и второго направлений. Разобьем их на 10 «уголков»: первый уголок — точки, лежащие на первых прямых первого и второго направления. Второй — лежащие на вторых прямых (кроме точек, лежащих в первом уголке) и т.д. Количество точек пересечения прямых в уголках — 19, 17, …, 1. Треугольники со сторонами, параллельными двум выбранным направлениям, бывают двух ориентаций, причем каждая из наших 100 точек может быть вершиной не более одного треугольника каждой ориентации. Поэтому, 10 прямых третьего направления образуют не более 10 • 2 • 5 треугольников с первыми пятью «уголками». Заметим далее, что каждая из прямых третьего направления образует не более одного треугольника каждой ориентации с точками уголка, поэтому треугольников с остальными пятью «уголками» будет не больше 2 • 25, т.к. на них всего 25 точек пересечения прямых первых двух направлений. Итого треугольников не более 100 + 50 = 150. Пример со 150 треугольниками см. на рис..iv01.118
Задача 5: a, b и c — целые числа, c ≠ b. Известно, что квадратные трехчлены ax² + bx + c и (c – b)x² + (c – a)x + (a + b) имеют общий корень (не обязательно целый). Докажите, что a + b + 2c делится на 3.
(А.Храбров)
Решение: Вычтем из первого трехчлена второй. Получим, что они оба имеют общий корень с трехчленом ax²\!\! + bx + c – ((c – b)x²\!\! + (c – a)x + (a + b)) = (a + b – c)(x²\!\! + x – 1). Следовательно, либо a + b – c = 0, либо их общий корень совпадает с одним из корней трехчлена x² + x – 1. В первом случае имеем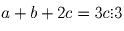 .
Во втором случае получаем, что если x0 — общий корень трехчленов
ax² + bx + c = 0 и x² + x – 1 = 0, то
.
Во втором случае получаем, что если x0 — общий корень трехчленов
ax² + bx + c = 0 и x² + x – 1 = 0, то 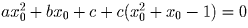 ,
откуда ((a + c)x0 + (b + c))x0 = 0. Число x0 — иррационально, поэтому
полученное равенство возможно только если a + c = 0 и b + c = 0, т.е. a = b = – c
и, следовательно a + b + 2c = 0, что делится на 3.
Задача 6:
Дан треугольник ABC. На прямой AC отмечена точка B1 так, что AB = AB1,
при этом B1 и C находятся по одну сторону от A. Через точки C, B1 и
основание биссектрисы угла A треугольника ABC проводится окружность ω ,
вторично пересекающая окружность, описанную около треугольника ABC, в точке Q.
Докажите, что касательная, проведенная к ω в точке Q, параллельна AC.
,
откуда ((a + c)x0 + (b + c))x0 = 0. Число x0 — иррационально, поэтому
полученное равенство возможно только если a + c = 0 и b + c = 0, т.е. a = b = – c
и, следовательно a + b + 2c = 0, что делится на 3.
Задача 6:
Дан треугольник ABC. На прямой AC отмечена точка B1 так, что AB = AB1,
при этом B1 и C находятся по одну сторону от A. Через точки C, B1 и
основание биссектрисы угла A треугольника ABC проводится окружность ω ,
вторично пересекающая окружность, описанную около треугольника ABC, в точке Q.
Докажите, что касательная, проведенная к ω в точке Q, параллельна AC.
(Л.Емельянов)
Решение: Пусть A1 — основание биссектрисы угла A. Так как точки B и B1 симметричны относительно AA1, то ∠ ABA1 = ∠ AB1A1 = ∠ AQ1C, где Q1 — точка пересечения AA1 с описанной окружностью. Значит, точки B1, C, A, Q1 лежат на одной окружности, т.е. Q = Q1.Отсюда следует, что Q — середина дуги BC, т.е. QB = QC, кроме того, точки B и B1 симметричны относительно AQ, значит, QB1 = QB = QC, т.е. ∆ CQB1 — равнобедренный и касательная к его описанной окружности, проведенная в вершине, параллельна основанию.
Задача 7: Множество клеток на клетчатой плоскости назовем ладейно связным, если из любой его клетки можно попасть в любую другую, двигаясь по клеткам этого множества ходом ладьи (ладье разрешается перелетать через поля, не принадлежащие нашему множеству). Докажите, что ладейно связное множество из 100 клеток можно разбить на пары клеток, лежащих в одной строке или в одном столбце.
(И.Певзнер)
Решение: Индукцией по n докажем утверждение задачи для любого ладейно связного множества, состоящего из 2n клеток. База (n = 1) очевидна.Будем называть пары клеток, лежащих в одной строке или
в одном столбце, «доминошками». Попробуем удалить какую-нибудь
доминошку, состоящую, для определенности, из клеток A и B, лежащих
в одной строке. При удалении множество может распасться не более чем на
три ладейно связных подмножества M, N, L, первое из которых остается
связным при добавлении клетки A, второе — при добавлении клетки
B, а третье — при добавлении любой из этих двух клеток
(возможно, некоторые из этих множеств пусты). Если все
эти множества состоят из четного числа клеток, удалим доминошку AB
и применим предположение индукции к этим множествам. Если, скажем, во множествах
M и N количества клеток нечетны, то они непусты и количество клеток
в каждом из них не превосходит 2n – 3, а количество клеток в множестве L
четно и не превосходит 2n – 2. Тогда можно применить предположение
индукции к множествам 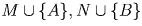 и L. Остальные
случаи четности разбираются аналогично.
и L. Остальные
случаи четности разбираются аналогично.
(В.Сендеров)
Решение: Ответ: 2001. Докажем, что числа на окружности не превосходят 2001.Лемма 1. Пусть x и y — натуральные числа. Если xy = x + y, то x = y = 2, а если xy < x + y, то хотя бы одно из чисел x, y равно 1.
Для доказательства достаточно переписать неравенство xy ≤ x + y в виде (x – 1)(y – 1) ≤ 1.
Лемма 2. Если xy = c, где x > 0, y > 0, x ≤ y, то сумма x + y убывает при возрастании x.
Утверждение леммы следует из убывания функции 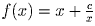 ,
где c > 0, на интервале
,
где c > 0, на интервале 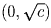 .
.
Поделим сумму чисел каждой пары на произведение чисел, следующей (по часовой
стрелке) пары и перемножим полученные частные. По условию мы получим целое число.
С другой стороны, это произведение есть произведение чисел вида 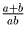 .
Отсюда и из Леммы 1 следует, что если хотя бы одна пара отлична от (2,2), то
найдется пара вида (1,k). Начнем с этой пары и будем перемещаться по окружности
по часовой стрелке.
.
Отсюда и из Леммы 1 следует, что если хотя бы одна пара отлична от (2,2), то
найдется пара вида (1,k). Начнем с этой пары и будем перемещаться по окружности
по часовой стрелке.
Первый случай.
Последующие пары имеют вид: (1,k + 1), (1,k + 2), …,(1,k + 999).
Значит, 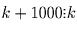 , откуда
, откуда 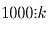 . Но тогда
. Но тогда
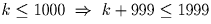 .
.
Второй случай. Найдется пара вида (1,l) такая, что следующая пара (a,b) отлична от (1,l + 1).
По условию ab — делитель числа s1 = 1 + l. Если ab = l + 1, то по Лемме 2
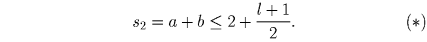
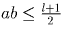 , то по Лемме 2
, то по Лемме 2
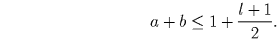
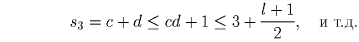
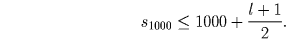
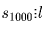 , значит, s1000 ≥ l. Последние два
неравенства дают: l ≤ 2001. Тогда из приведенных выше оценок следует, что для любой
последующей (1,l) пары s ≤ 2001. Значит, каждое число в этих парах не
превосходит 2000.
, значит, s1000 ≥ l. Последние два
неравенства дают: l ≤ 2001. Тогда из приведенных выше оценок следует, что для любой
последующей (1,l) пары s ≤ 2001. Значит, каждое число в этих парах не
превосходит 2000.Таким образом, оценка 2001 доказана. Метод доказательства позволяет указать ситуацию, в которой эта оценка достигается.
| Задачная база >> Соревнования всероссийского уровня >> Зональный этап всероссийской олимпады. >> XXVII >> 10 класс | Убрать решения |