Задача 1:

Задача 2: Петя и Коля играют в следующую игру: они по очереди изменяют один из коэффициентов a или b квадратного трехчлена f = x² + ax + b: Петя на 1, Коля — на 1 или на 3. Коля выигрывает, если после хода одного из игроков получается трехчлен, имеющий целые корни. Верно ли, что Коля может выиграть при любых начальных целых коэффициентах a и b независимо от игры Пети?

(Н.Агаханов)

Решение: Ответ: Верно.

Решение 1. Вначале Коля будет изменять коэффициент b до тех пор, пока b не попадет в промежуток [ – 2,0]. Петя ходами в 1 не сможет помешать ему сделать это.

Теперь если 1) b = 0, то Коля выиграл (трехчлен f = x² + ax имеет целые корни); 2) b =  – 1, то Петя, чтобы не проиграть, должен получить b =  – 2, так как если он оставит b =  – 1, то следующим ходом Коля сделает b = 0.

Итак, получен коэффициент b =  – 2 и Петя не может изменять его, так как коэффициент b =  – 1 или b =  – 3 Коля своим ходом сразу превратит в 0.

Далее Коля будет изменять на 3 коэффициент a до тех пор, пока тот не попадет в промежуток  – 1,1.

Если a =  ± 1, то он выиграл: трехчлен f = x² ± x – 2 имеет целые корни. Если же a = 0, то следующим ходом уже Петя получит такой трехчлен.

Решение 2. Покажем, что Коля всегда может получить трехчлен, один из корней которого равен 2. Тогда из теоремы Виета (x₁ + x₂ =  – a) будет следовать, что и второй корень — целый. Для этого ему нужно добиться равенства: f(2) = 4 + 2a + b = 0, т.е. 2a + b =  – 4. Но Петя может изменять выражение A = 2a + b на  ± 2 (изменив a), либо на  ± 1, изменив b, а Коля — на  ± 2,  ± 6,  ± 1,  ± 3. Изменяя b на  ± 3, Коля может получить A ∈ [ – 3, – 5]. Из A =  – 3 Петя получит A =  – 5,  – 1 ,  – 4 (проигрыш),  – 2 и следующим ходом Коля получит A =  – 4.

Из A =  – 5 Петя получит A =  – 3,  – 7,  – 4 (проигрыш),  – 6 и Коля получает A =  – 4.

Задача 3: В параллелограмме ABCD на сторонах AB и BC выбраны точки M и N соответственно так, что AM = NC, Q — точка пересечения отрезков AN и CM. Докажите, что DQ — биссектриса угла D.

(Л.Емельянов)

Решение: Пусть P — точка пересечения прямых AN и DC (см. рис.). Тогда утверждение задачи равносильно следующему равенству: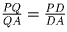 . Пусть AB = CD = a, AD = BC = b, AM = CN = c и CD = x. Тогда из подобия треугольников NCP и ADP следует 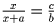, откуда 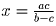и 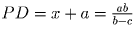. Далее, из подобия треугольников AMQ и PCQ следует 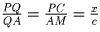. Утверждение задачи следует из равенства

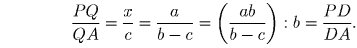
iv01.93

Задача 4: Мишень представляет собой треугольник, разбитый тремя семействами параллельных прямых на 100 равных правильных треугольничков с единичными сторонами. Снайпер стреляет по мишени. Он целится в треугольничек и попадает либо в него, либо в один из соседних с ним по стороне. Он видит результаты своей стрельбы и может выбирать, когда стрельбу заканчивать. Какое наибольшее число треугольничков он может с гарантией поразить ровно пять раз.

(Ю.Лифшиц)

Решение: Ответ: 25. I) Стратегия: рассмотрим разбиение мишени на 25 треугольных кусков 2 × 2, т.е. состоящие из четырех треугольников (см. рис.). Тогда стреляя в центр каждого из них до тех пор, пока в одном из четырех треугольников куска не накопится пять попаданий, он получит ровно 25 «призовых мишеней». II) Если при стрельбе в какой-то треугольничек какого-то куска стрелок всегда будет попадать в центральный треугольничек этого куска, то «призовых» мишеней будет не больше 25-и, т.к. в остальные он не попадет ни разу.

iv01.84

Задача 5: В выпуклом пятиугольнике выбраны две точки. Докажите, что можно выбрать четырехугольник с вершинами в вершинах пятиугольника так, что в него попадут обе выбранные точки.

(В.Дольников)

Решение: Решение 1. Рассмотрим в нашем пятиугольнике ABCDE 5 треугольников: ABC, BCD, CDE, DEA, EAB (см. рис.).

Тогда любая точка лежит не более, чем в двух треугольниках, следовательно есть треугольник, в котором нет наших точек. Отрезаем его и получаем разрез, удовлетворяющий условию.

Решение 2. Проведем прямую через эти точки. В одной из полуплоскостей лежит три вершины пятиугольника (из которых хотя бы две не лежат на этой прямой). Отрезаем этот треугольник и получаем нужное разбиение.

iv01.95

Задача 6: Существует ли такое натуральное число, что произведение всех его натуральных делителей (включая 1 и само число) оканчивается ровно на 2001 ноль?

(А.Храбров)

Решение: Ответ: Существует. Например, 5 • 2²ººº или 2 • 5²ººº.

Покажем, что первое число подходит. Для этого выпишем все его делители, кратные пяти:

Их произведение будет делиться на 5 в 2001 степени и не будет делиться на 5 в 2002 степени. Следовательно, произведение всех делителей числа 5 • 2²ººº будет кратно 10 в 2001 степени и не кратно 5 • 10²ºº¹. Поэтому оно оканчивается ровно на 2001 ноль.

Задача 7: Окружность, вписанная в угол с вершиной O, касается его сторон в точках A и B, K — произвольная точка на меньшей из двух дуг AB этой окружности. На прямой OB взята точка L такая, что прямые OA и KL параллельны. Пусть M — точка пересечения окружности  ω , описанной около треугольника KLB, с прямой AK, отличная от K. Докажите, что прямая OM касается окружности  ω .

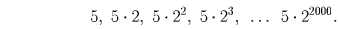
(С.Берлов, П.Кожевников)

Решение: Пусть  ∠ OAK =  α . Из параллельности LK || OA следует:  ∠ LKM =  ∠ OAK =  α . По теореме об угле между касательной и хордой:  ∠ KBA =  ∠ OAK =  α . Так как углы LKM и LBM вписаны в окружность  ω  и опираются на одну дугу, то  ∠ LBM =  ∠ LKM =  α .

Из равенства углов  ∠ OAM =  ∠ OBM =  α  следует, что четырехугольник OABM — вписанный. Отсюда  ∠ OMA =  ∠ OBA. Но  ∠ OBA =  ∠ KBM, так как  ∠ KBA =  ∠ OBM =  α . Значит,  ∠ OMA =  ∠ KBM, откуда по обратной теореме о касательной и хорде получаем, что OM касается окружности  ω  в точке M.

iv01.97

Задача 8: Саша написал на доске ненулевую цифру и приписывает к ней справа по одной ненулевой цифре, пока не выпишет миллион цифр. Докажите, что на доске не более 100 раз был написан точный квадрат.

(А.Голованов)

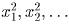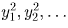Решение: Рассмотрим отдельно числа из нечетного и из четного числа знаков. Пусть — встретившиеся на доске квадраты из четного количества знаков, и в их записи содержится соответственно 2n₁,2n₂, … (n₁ < n₂ <  … ) цифр. Аналогично, пусть — встретившиеся на доске квадраты из нечетного количества знаков, и в их записи содержится соответственно 2m₁ – 1,2m₂ – 1, … (m₁ < m₂ <  … ) цифр.

Число 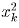содержит n_k цифр и не оканчивается на 0, поэтому 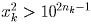, откуда 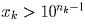. Число 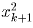получается из x_k приписыванием некоторого четного количества – обозначим его 2a — ненулевых цифр. Поэтому 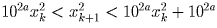. Из левого неравенства получаем 10^ax_k + 1 ≤ x_k + 1, следовательно, 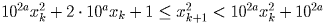, откуда 2 • 10^ax_k + 1 < 10^2a, т.е. x_k < 10^a. Из этого неравенства следует, что x_k содержит не более a цифр, т.е. n_k ≤ a, тогда из неравенства 10^ax_k + 1 ≤ x_k + 1 следует a + n_k ≤ n_k + 1, откуда 2n_k ≤ n_k + 1.

Аналогичное рассуждение применимо к последовательности y_k: 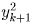получается приписыванием к 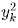2a цифр, y_k < 10^a, и a ≥ m_k, то есть m_k + 1 ≥ 2m_k. Теперь заметим, что в каждой из последовательностей m_k и n_k меньше 50 членов (так как m₁,n₁ ≥ 1 и m₅₀ и n₅₀ должны быть не меньше, чем 2⁵⁰ > 1000000).

Итак, всего квадратов на доске окажется не более 100.