Задача 1:
Построить график уравнения:
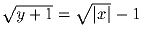
.
Задача 2:
В вершинах куба записаны 8 неотрицательных чисел.
Известно, что сумма любых двух соседних чисел не больше 2.
Найти наибольшее возможное значение суммы каких-либо семи из
этих чисел.
Задача 3:
В параллелограмме ABCD на сторонах AB, BC, CD, DA взяты
точки K, L, M, N соответственно. Известно, что площадь
четырехугольника KLMN в 2 раза меньше площади
параллелограмма ABCD. Докажите, что KM\|AD или LN\|AB.
Задача 4:
Доказать, что для любого
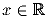
справедливо
неравенство:
| cos x| + | cos 2x| + | cos 4x| + … + | cos 2
1991x| ≥ 498
Задача 5:
На доске выписаны все натуральные числа от 1 до k.
разрешается на n-ом ходу вместо любых двух написанных чисел
написать их сумму, если n нечетно, и модуль их разности,
если n четно, и так до тех пор, пока на доске не останется
одно число (1 ≤ n ≤ k). Какое наименьшее число может остаться на
доске?


 .
.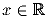 справедливо
неравенство:
| cos x| + | cos 2x| + | cos 4x| + … + | cos 21991x| ≥ 498
Задача 5:
На доске выписаны все натуральные числа от 1 до k.
разрешается на n-ом ходу вместо любых двух написанных чисел
написать их сумму, если n нечетно, и модуль их разности,
если n четно, и так до тех пор, пока на доске не останется
одно число (1 ≤ n ≤ k). Какое наименьшее число может остаться на
доске?
справедливо
неравенство:
| cos x| + | cos 2x| + | cos 4x| + … + | cos 21991x| ≥ 498
Задача 5:
На доске выписаны все натуральные числа от 1 до k.
разрешается на n-ом ходу вместо любых двух написанных чисел
написать их сумму, если n нечетно, и модуль их разности,
если n четно, и так до тех пор, пока на доске не останется
одно число (1 ≤ n ≤ k). Какое наименьшее число может остаться на
доске?