ЗАБА Математические олимпиады и олимпиадные задачи
Задачная база >> Украинские соревнования >> Харьковские соревнования >> Областные олимпиады >> 1991 >> 11 классУбрать решения
Харьковские областные олимпиады. 1991. 11 класс

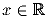Задача 1: При каком значении параметра a неравенство a(a – 1)x² + 2ax + 2 > 0 справедливо при всех ?

Задача 2:

Задача 3: В трапеции ABCD (AD\|BC) проведены биссектрисы внешних углов A и B до пересечения в точке E и биссектрисы внешних углов C и D до пересечения в точке F. Известно, что EF = 10 см. Найти периметр трапеции ABCD.

Задача 4: Доказать, что уравнение x² + y² + z² = 19901991 не имеет решений в целых числах.

Задача 5:

Задачная база >> Украинские соревнования >> Харьковские соревнования >> Областные олимпиады >> 1991 >> 11 классУбрать решения