Задача 1: Решить систему уравнений

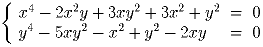
Задача 2: Многочлен P(x) = x³ + ax² + bx обладает тем свойством, что при любом c уравнение P(x) = c имеет ровно 1 решение. Доказать, что a² ≤ 3b.

Задача 3: На сторонах AB и BC треугольника ABC во внешнюю сторону построены квадраты ABDK и CBEL. Доказать, что продолжение высоты BH треугольника ABC служит медианой треугольника DBE.

Задача 4: Доказать, что любое натуральное число, большее 100, можно представить в виде суммы не более чем 9 натуральных чисел, в десятичной записи которых могут участвовать только цифры 0, 3 и 7.

Задача 5: В таблице N × N расставлены неотрицательные числа. Известно, что если на пересечении строки и столбца стоит 0, то сумма всех чисел в этих строке и столбце не меньше N. Доказать, что сумма всех чисел в таблице не меньше .
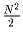
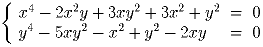
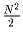