Задача 1:
Число X является корнем некоторого кубического
уравнения. Известно, что если все коэффициенты этого
уравнения увеличить на 1992, то X также будет корнем
получившегося уравнения. Найти X.
Задача 2:
В треугольнике со сторонами a ≤ b ≤ c выбрали две
произвольные точки M и N. Докажите, что MN ≤ c.
Задача 3:
Решить в целых числах уравнение
1991x² + 1992y² = 1993z²
Задача 4:
Докажите, что если все вершины выпуклого n-угольника
лежат в узлах клетчатой бумаги, а внутри и на его сторонах
других узлов нет, то
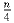
.
Задача 5:
Найти все многочлены F(x) такие, что
F(x + y) = F(x) + F(y) + 5xy(x + y)³ – 5x²y²(x + y)
при всех x, y и F(1) = 1992.


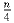 .
.