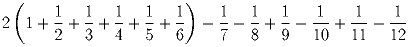Задача 1: Доказать, что если хотя бы одно из натуральных чисел a и b отлично от 1, то выполняется неравенство 3(a² + b²) ≥ 5(a + b).

Задача 2: На стадионе по трём параллельным дорожкам с постоянными скоростями движутся спортсмены A, B, C. В начальный момент времени площадь треугольника ABC равнялась 2 м² , а через 5 секунд она составляла 3 м². Какой станет эта площадь ещё через 5 секунд?

Задача 3: Пусть n — натуральное число. Может ли сумма цифр числа M = (n + 1)² + (n + 2)² +  …  + (n + 1980)² равняться 1981?

Задача 4: В параллелограмм A₁A₂A₃A₄ вписан четырёхугольник B₁B₂B₃B₄ так, что B₁ ∈ A₁A₂, B₂ ∈ A₂A₃, B₃ ∈ A₃A₄, B₄ ∈ A₄A₁ и

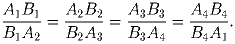
Доказать, что четырёхугольник B₁B₂B₃B₄ — параллелограмм, и что его центр совпадает с центром параллелограмма A₁A₂A₃A₄.

Задача 5: Часть клеток бесконечного листа бумаги в клетку покрашена в белый цвет, а остальные — в красный. Назовём клетку особенной, если её цвет отличается от цвета хотя бы одной из восьми соседних клеток. Доказать, что всегда найдётся хотя бы девять особенных клеток.

Задача 6: Доказать, что после приведения к общему знаменателю выражения

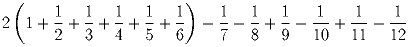
его числитель разделится на 13.