 |
 |
|
| Задачная база >> Украинские соревнования >> Всеукраинская олимпиада школьников >> 1983, Ужгород >> 10 класс | Убрать решения |
|
|
| Украинские соревнования. Всеукраинская олимпиада школьников. 1983, Ужгород. 10 класс |
|
|
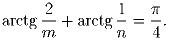
Задача 2: Паркет, покрывающий плоскость, состоит из правильных треугольников. Можно ли, используя 4 краски, раскрасить паркет так, чтобы каждый его треугольничек был закрашена в один цвет, а любые 4 треугольничка, образующие правильный треугольник, были разного цвета?
Задача 3: Каким соотношениям должны удовлетворять коэффициенты уравнения x4 + ax³ + bx² + cx + d = 0, чтобы после некоторых тождественных преобразований и последующей замены переменной
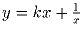 заданное уравнение сводилось к квадратному?
заданное уравнение сводилось к квадратному?Задача 4:
Задача 5: Найти множество вершин всех парабол на координатной плоскости xOy, имеющих общую касательную с параболой y = x² в точке A(a;a²).
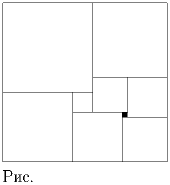
Задача 6: Прямоугольник разбит на квадраты так, как показано на рисунке. Известно, что площадь заштрихованного квадрата равна 1. Найти площадь прямоугольника.
Задача 7: Последовательность an ограничена и для любого n ≥ 3 выполняется неравенство an ≤ 3an – 1 – 3an – 2 + an – 3. Доказать, что эта последовательность сходящаяся.
Задача 8: Из точки O, расположенной внутри куба и не лежащей ни в одном из диагональных сечений, параллельно одной из диагоналей куба выпущен световой луч. Доказать, что отразившись по одному разу от каждой грани куба, луч вернется в точку O.
| Задачная база >> Украинские соревнования >> Всеукраинская олимпиада школьников >> 1983, Ужгород >> 10 класс | Убрать решения |