 |
 |
|
| Задачная база >> Украинские соревнования >> Всеукраинская олимпиада школьников >> 1983, Ужгород >> 8 класс | Убрать решения |
|
|
| Украинские соревнования. Всеукраинская олимпиада школьников. 1983, Ужгород. 8 класс |
|
|
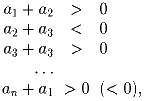
Задача 2: Задача 3: Существует ли треугольник, длины двух биссектрис которого не превышают 1, а площадь больше 1983?
Задача 4: Задача 5: Решить систему уравнений
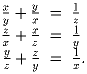
Задача 6: В трапеции ABCD сумма внутренних углов, примыкающих к основанию AD, равна 90. Обозначим через K и L середины оснований трапеции, а через M и N — середины её диагоналей. Доказать, что MN = KL.
Задача 7: На доске в строку выписаны 105 единиц. У каждой третьей из них изменили знак, затем у каждого пятого из полученных чисел также изменили знак, после этого знак изменили у каждого седьмого числа. Чему равна сумма полученых чисел?
Задача 8: Прямоугольник разбит на квадраты так, как показано на рис . Известно, что площадь заштрихованного квадрата равна 1. Найти стороны прямоугольника.

| Задачная база >> Украинские соревнования >> Всеукраинская олимпиада школьников >> 1983, Ужгород >> 8 класс | Убрать решения |