 |
 |
|
| Задачная база >> Украинские соревнования >> Всеукраинская олимпиада школьников >> 1983, Ужгород >> 9 класс | Убрать решения |
|
|
| Украинские соревнования. Всеукраинская олимпиада школьников. 1983, Ужгород. 9 класс |
|
|
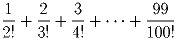
Задача 2: В некотором городе все дороги состоят из сторон треугольника ABC и отрезков, соединяющих его вершины с точкой пересечения биссектрис O. Путешественник находится в пункте O и намерен побывать в пунктах A, B, C и вернуться в O (двигаясь по дорогам). Как выбрать кратчайший маршрут для этого путешествия?
Задача 3: На координатной плоскости от начала координат отложены n векторов, сумма которых — нулевой вектор. Доказать, что эти векторы можно перенумеровать так, чтобы все суммы
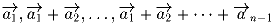
Задача 4: На продолжении стороны AB треугольника ABC выбрана точка A такая, что AO = 2AB. Через точку O проведеная прямая, пересекающая стороны AC и BC соответственно в точках K и L. Найти предел отношения площади треугольника OBL к площади четырёхугольника AKLB, когда длина отрезка AK стремится к нулю.
Задача 5: Многочлен четвёртой степени имеет четыре корня, попарные расстояния между которыми не меньше 1. Доказать, что производная этого многочлена имеет хотя бы два корня, расстояние между которыми также не меньше 1.
Задача 6: Задача 7: Пусть ABCD — выпуклый четырёхугольник. От некоторой точки O откладываются четыре вектора
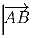 ,
, 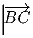 ,
,
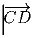 и
и 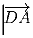 , концы которых обозначим B1, C1, D1,
A1 соответственно. Всегда ли четырёхугольник A1B1C1D1
выпуклый? Вычислить его площадь, если площадь исходного
четырёхугольника равна S.
, концы которых обозначим B1, C1, D1,
A1 соответственно. Всегда ли четырёхугольник A1B1C1D1
выпуклый? Вычислить его площадь, если площадь исходного
четырёхугольника равна S.Задача 8: По заданной тройке чисел a0 ≥ b0 ≥ c0 образуем разности a0 – b0, a0 – c0, b0 – c0 . Упорядочив их по убыванию, получим новую тройку a1 ≥ b1 ≥ c1 . По ней тем же способом строятся числа a2, b2, c2 и т.д. (Например, для тройки a0 = 8, b0 = 7, c0 = 3 получим a1 = 8 – 3 = 5, b1 = 7 – 3 = 4, c1 = 8 – 7 = 1, a2 = 4, b2 = 3, c2 = 1 и т.д.) Известно, что a0 = 1. При каких b0 и c0 число a10 будет наименьшим?
| Задачная база >> Украинские соревнования >> Всеукраинская олимпиада школьников >> 1983, Ужгород >> 9 класс | Убрать решения |