 |
 |
|
| Задачная база >> Украинские соревнования >> Всеукраинская олимпиада школьников >> 1984, Херсон >> 10 класс | Убрать решения |
|
|
| Украинские соревнования. Всеукраинская олимпиада школьников. 1984, Херсон. 10 класс |
|
|
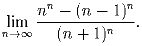
Задача 2: Найти углы между векторами
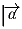 ,
, 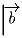 и
и  в пространстве, если известно, что углы эти попарно равны и
в пространстве, если известно, что углы эти попарно равны и
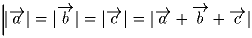 .
.Задача 3: Задача 4: На круге последовательно через 120 записаны числа 1, 2 и 3. Круг прикреплен к доске так, что он может поворачиваться вокруг своего центра на углы, кратные 120. Вначале рядом с каждым числом 1, 2 и 3 на доске написан нуль. Разрешается поворачивать круг несколько раз и после каждого поворота к каждому из написанных на доске чисел прибавить то число, которое оказалось рядом с ним на круге. Можно ли в результате получить на доске числа 15, 14, 13, записанные в том же порядке, что и числа 1, 2, 3 на круге?
Задача 5: Доказать, что число 101 нельзя представить в виде суммы девяти попарно взаимно простых натуральных чисел, отличных от 1.
Задача 6: На прямой последовательно расположены 9 точек
 .
Найти на этой прямой точку A, сумма расстояний от которой до данных
точек наименьшая.
.
Найти на этой прямой точку A, сумма расстояний от которой до данных
точек наименьшая.Задача 7: Сколько решений имеет уравнение x = 6 sin (6 sin x)?
Задача 8: Сколько сторон может иметь выпуклый многоугольник единичной площади, если он имеет центр симметрии и в нём можно поместить треугольник, площадь которого 0,5?
| Задачная база >> Украинские соревнования >> Всеукраинская олимпиада школьников >> 1984, Херсон >> 10 класс | Убрать решения |