 |
 |
|
| Задачная база >> Украинские соревнования >> Всеукраинская олимпиада школьников >> 1985, Черновцы >> 10 класс | Убрать решения |
|
|
| Украинские соревнования. Всеукраинская олимпиада школьников. 1985, Черновцы. 10 класс |
|
|
Задача 2: Какое наибольшее число корней может иметь уравнение вида xn + ax² + bx + c = 0, где
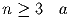 , b, c — заданные
числа?
, b, c — заданные
числа?Задача 3: На каждом из рёбер, выходящих из данной вершины единичного куба, взята точка на расстоянии a от вершины. Плоскость, проходящая через выбранные точки, отсекает от куба треугольную пирамиду. Известно, что если отсечь таким образом от куба 8 одинаковых пирамид (по одной от каждой вершины), то объём оставшейся части куба будет равен ½. Найти a (отсекаемые пирамиды могут пересекаться).
Задача 4:
Задача 5: Отрезки a, b, c являются сторонами некоторого треугольника. Доказать, что существует шестиугольник со сторонами
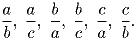
Задача 6: В последовательности xn x1 = 1, а каждое xn + 1 равно сумме цифр произведения xn на данное натуральное число m. Доказать, что при любом m эта последовательность, начиная с некоторого места, будет периодической.
Задача 7: В клетках квадратной таблицы 100 × 100 записаны какие-то числа. В некоторый момент каждое из этих чисел заменено на наибольшее из чисел, записанных в соседних клетках таблицы (соседними считаются клетки, имеющие общую сторону). Далее эту операцию выполним с новой таблицей, потом по тому же правилу получим ещё одну таблицу и т.д. а) Доказать, что в результате нескольких таких операций среди чисел таблицы будет не более двух различных. б) Может ли случиться так, что после нескольких таких операций все числа в таблице будут равны?
Задача 8: Функция f(x) определена на отрезке [\,0;1] и удовлетворяет уравнению f(x + f(x)) = f(x) для всех x ∈ [\,0;1]. Доказать, что f(x) = 0 для всех x ∈ [\,0;1].
| Задачная база >> Украинские соревнования >> Всеукраинская олимпиада школьников >> 1985, Черновцы >> 10 класс | Убрать решения |