 |
 |
|
| Задачная база >> Украинские соревнования >> Всеукраинская олимпиада школьников >> 1985, Черновцы >> 8 класс | Убрать решения |
|
|
| Украинские соревнования. Всеукраинская олимпиада школьников. 1985, Черновцы. 8 класс |
|
|
Задача 2: Обозначим через D(n) сумму всех делителей числа n (включая 1 и n). Для каких n число n • D(n) — нечётное?
Задача 3: На доске написаны числа дроби
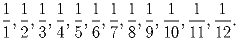
Задача 4:
Задача 5: Сколько существует целых чисел p, для которых уравнение x² + px + 1985 = 0 имеет целый корень?
Задача 6: Рациональное число
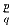 удовлетворяет условию
удовлетворяет условию
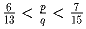 . Доказать, что q ≥ 28.
. Доказать, что q ≥ 28.Задача 7: Длина каждого звена замкнутой ломаной равна 1, а расстояние между любыми двумя её вершинами не превышает 1. Доказать, что эта ломаная имеет нечётное число звеньев.
Задача 8: В одном «не очень дружном» садово-огородном обществе (сокращённо СОО) каждые два соседних участка отгорожены друг от друга высокой стеной. Все участки квадратные и имеют одинаковую площадь, поэтому изображение СОО на плане напоминает лист бумаги в клетку. Садовод А включил на своём участке громкоговоритель. Звук слышен, если он проходит не более чем через 10 стен, но через 11 стен его уже не слышно. Доказать, что найдутся два садовода B и C, из которых B находится ближе к A, чем C, но при этом C слышит громкоговоритель, а B не слышит (считать, что громкоговоритель и садоводы находятся в центрах участков).
| Задачная база >> Украинские соревнования >> Всеукраинская олимпиада школьников >> 1985, Черновцы >> 8 класс | Убрать решения |