 |
 |
|
| Задачная база >> Украинские соревнования >> Всеукраинская олимпиада школьников >> 1986, Ровно >> 10 класс | Убрать решения |
|
|
| Украинские соревнования. Всеукраинская олимпиада школьников. 1986, Ровно. 10 класс |
|
|
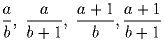
Задача 2: На параболе y = x² выбраны три точки A, B и C так, что угол ABC — прямой. Пусть a, b и c — абсциссы выбранных точек. Доказать, что (a + b)(b + c) = – 1.
Задача 3: Решить систему уравнений
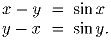
Задача 4: На плоскости проведена замкнутая 14-звенная ломаная, у которой каждые два соседних звена взаимно перпендикулярны. Какое наибольшее число точек самопересечения она может иметь?
Задача 5: О числах
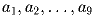 известно, что
известно, что
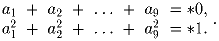
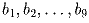 , чтобы выполнялось неравенство
, чтобы выполнялось неравенство
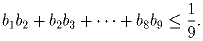
Задача 6: Задача 7: Всякий ли многочлен четвертой степени P(x) можно представить в виде P(x) = Q(R(x)), где Q(x) и R(x) — квадратные трехчлены?
| Задачная база >> Украинские соревнования >> Всеукраинская олимпиада школьников >> 1986, Ровно >> 10 класс | Убрать решения |