Задача 1:
Двадцать корзин расставлены по окружности. Можно ли разложить
в них 99 арбузов так, чтобы количества арбузов в любых двух
соседних корзинах отличались на единицу?
Задача 2:
Доказать, что сумма квадратов длин двух взаимно
перпендикулярных хорд, проходящих через фиксированную точку M
внутри круга, не зависит от положения этих хорд.
Задача 3:
Прямоугольник 20 × 30 разбит на единичные квадраты.
какое наибольшее число этих квадратов может пересекать прямая, не
проходящая через их вершины?
Задача 4:
Существует ли такое натуральное число n, что первые 8 цифр
дробной части (после запятой) числа
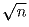
образуют число
19851986?
Задача 5:
Построить треугольник ABC, если известна его вершина A и
две прямые, на которых лежат медиана, проведенная из вершины B, и
биссектриса угла C.
Задача 6:
График квадратного трёхчлена y = ax² + bx + c с рациональными
коэффициентами параллельно сдвинули на вектор
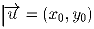
, координаты
которого также рациональные числа и x
0 ≠ 0. Доказать, что точка
пересечения этих двух графиков имеет рациональные координаты.
Задача 7:
На шахматной доске 8 × 8 в произвольном порядке
расставлены 32 белых и 32 чёрных пешки. Если из одной клетки на
другую можно пойти ходом шахматного коня, то пешки, стоящие на этих
клетках, можно переставить. Доказать, что при помощи нескольких
таких перестановок можно все белые пешки поставить на белые поля, а
чёрные пешки — на чёрные поля.
Задача 8:
Школьники едут в летний трудовой лагерь на 33 дня, из которых
6 должны быть выходными. Школьники хотели бы составить расписание
рабочих и выходных дней так, чтобы на каждые 12 дней подряд выпадало
не менее 3 выходных. Можно ли это сделать?


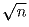 образуют число
19851986?
образуют число
19851986?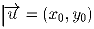 , координаты
которого также рациональные числа и x0 ≠ 0. Доказать, что точка
пересечения этих двух графиков имеет рациональные координаты.
, координаты
которого также рациональные числа и x0 ≠ 0. Доказать, что точка
пересечения этих двух графиков имеет рациональные координаты.