Задача 1:
Доказать, что для произвольных положительных чисел a, b, c, d
значение дроби
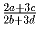
лежит между числами
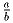
и
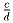
.
Задача 2:
Среди четырёх данных монет стоимостью 1, 2, 3 и 5 копеек находится
одна фальшивая. Фальшивая монета отличается от настоящей только массой, но
неизвестно, легче она или тяжелее настоящей. Настоящие монеты весят
соответственно 1, 2, 3 и 5 граммов. Можно ли двумя взвешиваниями на аптекарских
весах без гирь найти фальшивую монету?
Задача 3:
Множество натуральных чисел назовём «правильным», если для любых
двух чисел из этого множества некоторое их общее кратное также принадлежит
этому множеству. Множество всех натуральных чисел разбито на две части.
Доказать, что хотя бы одна из частей является «правильной».
Задача 4:
Киевское «Динамо» принимало участие в футбольном турнире, в котором
каждая команда сыграла равное число матчей. За каждую победу команде
начислялось 2 очка, за ничью — 1 очко, за поражение — ни одного. Известно,
что киевское «Динамо» набрало 90%, а каждая из остальных команд турнира
— не менее 40% возможного числа очков. Какое наименьшее число команд могло
участвовать в турнире (система проведения турнира может быть произвольной)?
Задача 5:
Шесть последовательно расположенных на окружности точек
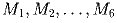
удовлетворяют условиям: M
1M
2 || M
4M
5, M
2M
3 || M
5M
6.
Доказать, что M
3M
4 || M
6M
1.
Задача 6:
Треугольник поделен на маленькие треугольнички так, как показано на
рисунке. В каждый из 15 узлов записано некоторое натуральное число так, что
сумма чисел в вершинах каждого маленького треугольничка оказалась нечётной.
Сколько среди 15 чисел может быть чётных (указать все возможные ответы)?


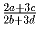 лежит между числами
лежит между числами 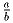 и
и 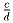 .
.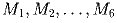 удовлетворяют условиям: M1M2 || M4M5, M2M3 || M5M6.
Доказать, что M3M4 || M6M1.
удовлетворяют условиям: M1M2 || M4M5, M2M3 || M5M6.
Доказать, что M3M4 || M6M1.