 |
 |
|
| Задачная база >> Украинские соревнования >> Всеукраинская олимпиада школьников >> 1987, Тернополь >> 8 класс | Убрать решения |
|
|
| Украинские соревнования. Всеукраинская олимпиада школьников. 1987, Тернополь. 8 класс |
|
|
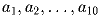 выполняется неравенство
выполняется неравенство
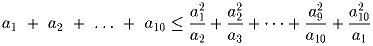
Задача 2: На бумаге в клетку с размером клеток 1 × 1 размещён многоугольник (не обязательно выпуклый), вершины которого лежат в узлах сетки, а стороны проходят только по сторонам и диагоналям клеток. Какую наибольшую площадь может иметь этот многоугольник, если его граница содержит 4n узлов сетки? Задача 3: Киевское «Динамо», набрав 90% возможного числа очков, победило в футбольном турнире. Все участники турнира сыграли одинаковое количество матчей, за каждую победу команде начислялось 2 очка, за каждую ничью — 1 очко, за поражение ни одного. Известно, что каждый участник турнира набрал не менее 80% очков команды, занявшей предыдущее место. Какое наименьшее число команд могло участвовать в турнире?
Задача 4: Обозначим через S фигуру, образующую совокупность концов L векторов вида
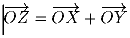 , где O — начало координат,
точка X пробегает все точки выпуклой фигуры S1, а точка Y — все точки
выпуклой фигуры S2 . Можно ли выбрать фигуры S1 и S2 так, чтобы каждая
из них содержала более одной точки и фигура S совпадала с данной трапецией
ABCD (все фигуры рассматриваются вместе со своими внутренними точками)?
, где O — начало координат,
точка X пробегает все точки выпуклой фигуры S1, а точка Y — все точки
выпуклой фигуры S2 . Можно ли выбрать фигуры S1 и S2 так, чтобы каждая
из них содержала более одной точки и фигура S совпадала с данной трапецией
ABCD (все фигуры рассматриваются вместе со своими внутренними точками)?Задача 5: Какие значения может принимать число x, если выполняются такие равенства:
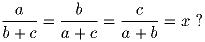
Задача 6: Можно ли на бумаге в клетку с размером клеток 1 × 1 разместить правильный треугольник со стороной 2 так, чтобы он не накрыл ни одного узла?
Задача 7: Для каких натуральных n число
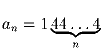 является точным квадратом?
является точным квадратом?Задача 8: В выпуклом четырёхугольнике ABCD окружности, вписанные в треугольники ABC и CDA, касаются. Доказать, что окружности, вписанные в треугольники BCD и DAB, также касаются.
| Задачная база >> Украинские соревнования >> Всеукраинская олимпиада школьников >> 1987, Тернополь >> 8 класс | Убрать решения |