Задача 1:
На шахматной доске размером 6 × 6 расставить 8 ферзей так,
чтобы каждый из них бил ровно 1 ферзя. Можно ли так расставить 9 ферзей?
Задача 2:
Доказать, что разносторонний треугольник нельзя разрезать прямой,
проходящей через его вершину, на два равных треугольника.
Задача 3:
Доказать, что для произвольного натурального числа n число n¹988 + n¹987 + 1 не является простым.
Задача 4:
Доказать, что число
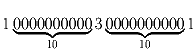
не является квадратом натурального числа.
Задача 5:
Доказать, что для произвольных положительных чисел a и b
выполняется неравенство
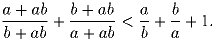
Задача 6:
Шесть фишек с номерами от 1 до 6 прикреплены к двум касающимся кругам
так, как это показано на рисунке (фишка с номером 3 прикреплена к обоим
кругам). Левый круг можно вращать вокруг центра в произвольном направлении на
углы, кратные 120, правый круг — на углы, кратные 90. При
вращении круга прикреплённые к нему фишки соответственным образом
переставляются. Доказать, что при помощи таких преобразований можно переставить
фишки в произвольном порядке.


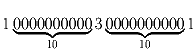 не является квадратом натурального числа.
не является квадратом натурального числа.