Задача 1: Какое наибольшее число клеток прямоугольной таблицы 19 × 89 можно покрасить в чёрный цвет так, чтобы в каждом квадрате 2 × 2 было не более двух чёрных клеток?

Задача 2:

Задача 3: Найти уравнение прямой, которая касается графика функции y = x⁴ + 6x³ + x² в двух точках.

Задача 4: Среди всех пирамид, образованных координатными плоскостями и касательной плоскостью к сфере x² + y² + z² = a², найти ту, которая имеет наименьший объём.

Задача 5: Решить уравнение x³ – 16x – 1989 = 0.

Задача 6: На доске написаны один за другим числа 7, 5, 5, 7. За ними записываем последнюю цифру суммы этих чисел, а первое число откидываем. Такую же операцию проделываем с полученными четырьмя числами, потом — с новой четвёркой и т. д. Можно ли получить на каком-то шаге четвёрку 1, 9, 8, 9?

Задача 7: Доказать, что для всех x из промежутка 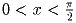и любого натурального n выполнено неравенство

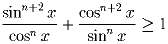
Задача 8: Можно ли внутри кубической коробки с ребром 1 разместить три правильных тетраэдра с ребром 1?