Задача 1: Аквариум, имеющий форму куба без верхней грани, нужно наполнить на 1/3 его объёма водой. Как это сделать, если разрешается лишь наклонять аквариум на произвольные углы и отливать из него воду в пустые ёмкости.

Задача 2: Доказать, что ни при каком значении параметра c уравнение x(x² – 1)(x² – 1989) = c не может иметь 5 целых корней.

Задача 3: Рассматривается сумма всех векторов 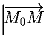с общим началом в точке M₀ и концами в точках M, которые принадлежат кругу x² + y² ≤ 9 и имеют целые координаты. Указать наибольшее и наименьшее возможное значение длины этой суммы в зависимости от положения точки M₀ (M₀ также принадлежит кругу).

Задача 4: Доказать, что для n неотрицательных чисел 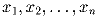, сумма которых равна n, выполняется неравенство:

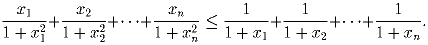
Задача 5: Пусть a, b, c — стороны треугольника, а R — радиус описанной около него окружности. Доказать, что a² + b² + c² ≤ 9R².

Задача 6: Внутри круга размещён пятиугольник A₁A₂A₃A₄A₅, у которого все стороны равны. Каждую из сторон пятиугольника продлим до пересечения с окружностью. Продолжения A₁A₂ за точку A₂, A₂A₃ за точку A₃, A₃A₄ за точку A₄, A₄A₅ за точку A₅ и A₅A₁ за точку A₁ покрасим в красный цвет, а остальные продолжения — в синий. Доказать, что сумма длин всех красных отрезков равна сумме длин всех синих отрезков.

Задача 7: Пусть x² – yz = a, y² – xz = b, z² – xy = c. Доказать, что ax + by + cz = (a + b + c)(x + y + z).

Задача 8: В лесу есть m • n тропинок и несколько полян. Каждая тропинка соединяет две поляны. Известно, что тропинки можно покрасить m цветами так, чтобы к каждой поляне сходились тропинки разных цветов. Доказать, что это можно сделать, покрасив каждым цветом ровно n тропинок.