 |
 |
|
| Задачная база >> Украинские соревнования >> Всеукраинская олимпиада школьников >> 1990, Днепропетровск >> 10 класс | Убрать решения |
|
|
| Украинские соревнования. Всеукраинская олимпиада школьников. 1990, Днепропетровск. 10 класс |
|
|
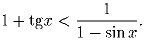
Задача 2:
Задача 3: Числа 105 последовательно выписаны в ряд. После этого изменён знак у каждого третьего числа, потом в полученной последовательности изменён знак у каждого пятого числа, и, наконец, в новой последовательности изменён знак у каждого седьмого числа. Найти сумму всех чисел в полученной последовательности.
Задача 4: На плоскости даны два одинаковых правильных n-угольника, которые пересекаются так, что образуется 2n-угольник, вообще говоря, неправильный. Стороны одного из n-угольников покрашены в красный цвет, второго — в синий. Доказать, что сумма квадратов всех синих сторон образованного 2n-угольника равна сумме квадратов его красных сторон.
Задача 5: Разложить на множители многочлен x4 + ax² + b, если известно, что a² < 4b.
Задача 6: Доказать, что сумма цифр числа 5317 меньше 1990.
Задача 7: Длина хорды AB окружности радиуса 1 меньше
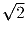 .
Прямая l, не пересекающая окружность, образует с прямой AB угол
45, внутри которого содержится центр окружности. Построить на
прямой l такую точку C чтобы в случае, когда DE — дуга,
отсекаемая на окружности углом ACB, прямая DE была
перпендикулярна прямой AB.
.
Прямая l, не пересекающая окружность, образует с прямой AB угол
45, внутри которого содержится центр окружности. Построить на
прямой l такую точку C чтобы в случае, когда DE — дуга,
отсекаемая на окружности углом ACB, прямая DE была
перпендикулярна прямой AB.Задача 8: Имеются 8 одинаковых кубиков с ребром 1. Произвольные 24 грани из всех 48 граней этих кубиков покрашены в белый цвет, а остальные 24 грани — в чёрный. Доказать, что из этих 8 кубиков можно сложить такой куб, что на его поверхности белых и чёрных квадратиков со стороной 1 будет поровну.
| Задачная база >> Украинские соревнования >> Всеукраинская олимпиада школьников >> 1990, Днепропетровск >> 10 класс | Убрать решения |