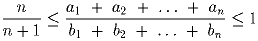Задача 1:
В каждой вершине куба сидела одна муха. Потом все мухи
взлетели и снова сели в некотором порядке по одной в каждую вершину.
Доказать, что найдутся три мухи, которые в начальном и в конечном
положении были вершинами равных треугольников.
Задача 2:
Задача 3:
На плоскости даны три луча с общим началом, разбивающие её на
три угла суммой 360. Внутри каждого угла отметили по точке.
Постройте при помощи циркуля и линейки треугольник, вершины которого
лежат на данных лучах (по одной на каждом) и стороны которого
проходят через отмеченные точки.
Задача 4:
Таблица с n строками и 6 столбцами, n ≥ 2, заполнена
нулями и единицами так, что все её строки различны и вместе с любыми
строками (

) и (
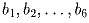
) в ней содержится и строка
(a
1b
1,a
2b
2, … ,a
6b
6). Доказать, что в некотором её
столбце не менее половины цифр — нули.
Задача 5:
На плоскости α выбрали произвольным образом точку A и
окружность γ . От каждой точки B окружности отложили перпендикуляр к
плоскости α , длина которого равна квадрату длины отрезка AB (все
перпендикуляры отложены в одну сторону от плоскости α ). Доказать, что
концы этих перпендикуляров лежат в одной плоскости.
Задача 6:
Даны 2n чисел из отрезка [1;2]. Доказать, что их можно
разбить на две группы —
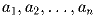
и
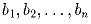
так, что
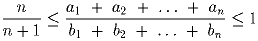
Задача 7:
Дана деревянная доска в клетку размером n × n. Двое игроков по очереди делают пилкой распилы длины 1,
идущие по линиям сетки. Каждый распил должен начинаться с узла сетки
на краю доски или на уже сделанном распиле. Проигрывает тот игрок,
после хода которого доска распадается на две части. Кто выиграет при
правильной игре: начинающий игру или его соперник?
Задача 8:


 ) и (
) и (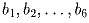 ) в ней содержится и строка
(a1b1,a2b2, … ,a6b6). Доказать, что в некотором её
столбце не менее половины цифр — нули.
) в ней содержится и строка
(a1b1,a2b2, … ,a6b6). Доказать, что в некотором её
столбце не менее половины цифр — нули.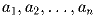 и
и 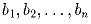 так, что
так, что