 |
 |
|
| Задачная база >> Украинские соревнования >> Всеукраинская олимпиада школьников >> 1992, Чернигов >> 10 класс | Убрать решения |
|
|
| Украинские соревнования. Всеукраинская олимпиада школьников. 1992, Чернигов. 10 класс |
|
|
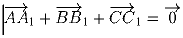 выполняется тогда и только тогда, когда треугольник ABC
правильный.
выполняется тогда и только тогда, когда треугольник ABC
правильный.Задача 3: Доказать, что не существует действительных чисел x, y, z, удовлетворяющих системе уравнений
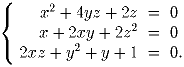
Задача 4: Дана конечная последовательность действительных чисел
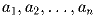 . Член ak этой последовательности назовём отмеченным,
если среди чисел ak, ak + ak + 1, …, ak + ak + 1 + … + an хотя бы одно положительно. Доказать, что сумма всех отмеченных
чисел положительна.
. Член ak этой последовательности назовём отмеченным,
если среди чисел ak, ak + ak + 1, …, ak + ak + 1 + … + an хотя бы одно положительно. Доказать, что сумма всех отмеченных
чисел положительна.Задача 5: Найти наибольшее натуральное значение n, для которого неравенство sin nx + cos nx > 1/2 выполняется для всех x из отрезка [\,0; π /2].
Задача 6: Точки A и B лежат на сторонах выпуклого многоугольника F, а точка A1 удовлетворяет соотношению
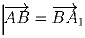 .
Обозначим через F1 выпуклый многоугольник наименьшей площади,
содержащий многоугольник F и точку A1. Доказать, что площадь
многоугольника F1 не больше удвоенной площади многоугольника F.
.
Обозначим через F1 выпуклый многоугольник наименьшей площади,
содержащий многоугольник F и точку A1. Доказать, что площадь
многоугольника F1 не больше удвоенной площади многоугольника F.Задача 7: Доказать, что для произвольных чисел a, b, c, d из отрезка [1;2] выполняется неравенство
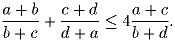
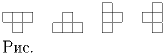
Задача 8: На шахматной доске 100 × 100 расположены 800 четырёхклеточных фигурок, имеющих форму буквы «T» в одной из возможных ориентаций (см.рис. ). Каждая такая фигурка полностью накрывает 4 клетки доски и никакие две фигурки не накрывают одну и ту же клетку. Доказать, что на доску можно положить ещё одну фигурку так, чтобы она полностью накрыла 4 свободные клетки.
| Задачная база >> Украинские соревнования >> Всеукраинская олимпиада школьников >> 1992, Чернигов >> 10 класс | Убрать решения |