 |
 |
|
| Задачная база >> Украинские соревнования >> Всеукраинская олимпиада школьников >> 1994, Херсон >> 10 класс | Убрать решения |
|
|
| Украинские соревнования. Всеукраинская олимпиада школьников. 1994, Херсон. 10 класс |
|
|
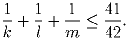
Задача 2: Найти наибольшее возможное значение выражения
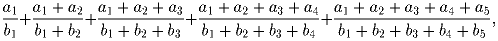
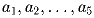 — произвольные числа из отрезка [1;2], а
— произвольные числа из отрезка [1;2], а 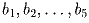 —
произвольная их перестановка.
—
произвольная их перестановка.Задача 3: На координатной плоскости xOy взят 1994-угольник (не обязательно выпуклый), все координаты вершин которого — целые числа, и все длины сторон которого также целые. Доказать, что его периметр — чётное число.
Задача 4: Внутри треугольника ABC взята точка D так, что углы DAC и DBC равны. Пусть K и L — основания перпендикуляров, опущенных из точки D на AC и на BC соответственно. Доказать, что середины отрезков AB, CD и KL лежат на одной прямой.
Задача 5: Выпуклый четырёхугольник площади 1 имеет две параллельные стороны. Найти наименьшее возможное значение длины его большей диагонали.
Задача 6: Последовательность натуральных чисел такова, что каждое следующее число больше предыдущего, но их разность меньше 1994. Доказать, что существует бесконечно много различных простых чисел, каждое из которых делит хотя бы один член этой последовательности.
Задача 7: Доска размером 2n × 2n состоит из единичных клеток. Можно ли половину из них закрасить в белый цвет, а половину — в чёрный так, чтобы в каждой строке и каждом столбце было не менее 75% клеток одного из цветов?
Задача 8:
| Задачная база >> Украинские соревнования >> Всеукраинская олимпиада школьников >> 1994, Херсон >> 10 класс | Убрать решения |