Задача 1: A и A + 1 — два 1994-значных числа, сумма цифр каждого из которых кратна 1994. а) Найти эти суммы цифр. б) Доказать, что количество таких пар чисел не меньше 100¹ºº.

Задача 2: Каждая из 1994² плиток 1 × 1 произвольно закрашена в один из k цветов. Нужно выложить мозаику 1994 × 1994 так, чтобы она была симметрична относительно одной из диагоналей. При каких k это всегда можно сделать?

Задача 3: Две окружности радиусов R и r касаются внутренним образом в точке M. Через произвольную точку A большей окружности проведена касательная к меньшей окружности, пересекающая большую окружность ещё раз в точке B. Найти наибольшее возможное значение периметра треугольников MAB.

Задача 4: Последовательность a_n задана соотношениями:

При каких значениях a эта последовательность ограничена?

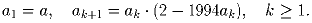
Задача 5: Пусть n — натуральное число, а D(n) — произведение цифр числа n. Решить уравнение

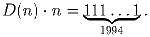
Задача 6: Пусть a₁ — наименьшее натуральное число, для которого 1/a₁ < 1, a₂ — наименьшее натуральное число, для которого 1/a₁ + 1/a₂ < 1, a₃ — наименьшее натуральное число, для которого 1/a₁ + 1/a₂ + 1/a₃ < 1. Доказать, что при любом натуральном n выполняется равенство

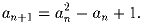
Задача 7: В пространстве даны точки P, Q, S. Из каждой из точек P и Q проведены по два луча так, что каждая пара лучей пересекается. Известно, что точки A, B, C, D пересечения этих лучей образуют четырёхугольник единичной площади, и от пирамиды SABCD некоторой плоскостью можно отрезать пирамиду SKLMN, основание KLMN которой — прямоугольник. Доказать, что объём пирамиды SABCD не превышает .

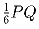Задача 8: Олимпиада проходит в два тура, и перед жюри стоит задание: в каждом туре рассадить участников олимпиады в аудиториях так, чтобы любые два участника хотя бы во время одного из туров сидели в аудиториях с различным числом участников. Может ли жюри сделать это, если в олимпиаде принимает участие а) 9 учеников; б) 14 учеников?