 |
 |
|
| Задачная база >> Разное >> Задачник первого-второго года обучения >> Делимость | Показать решения |
|
|
| Математический кружок. Задачник первого-второго года обучения. Делимость |
|
|
Задача 2: Может ли произведение цифр натурального числа равняться 1980?
Задача 3: Доказать,что дробь
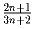 несократима.
несократима.Задача 4: a и b – натуральные числа, такие, что 34a = 43b. Доказать, что a + b – составное число.
Задача 5: Существует ли натуральные a,b, такие, что ab(a + b) = 15015?
Задача 6: Может ли произведение четырех последовательных натуральных чисел быть равно 11880 ?
Задача 7: a) На сколько нулей оканчивается 100!?
b) Четна или нечетна последняя ненулевая цифра 100!?
Задача 8: Найти минимальное n, такое, что n! делится на 1080.
Задача 9: Существуют ли 13 натуральных чисел с суммой 1990 и произведением 198919891989?
Задача 10: a + b делится на k, ab делится на k. Доказать, что
a) a² + b² делится на k
b) a³ + b³ делится на k².
Задача 11: Доказать, что нет целых a,b,c,d,e, таких что ab = bc = cd = de = ea = 30.
Задача 12: Доказать, что число делителей n нечетно тогда и только тогда, когда n – точный квадрат.
Задача 13: Доказать, что простых чисел бесконечно много.
Задача 14: Доказать, что среди натуральных чисел есть 100 составных подряд. Задача 15: a,b,k – целые числа. a + b и ab делятся на k. Доказать, что
a) a² – b² делится на c.
b) a² + b² делится на k
c) a³ + b³ делится на k².
Задача 16: Доказать, что дроби не сократимы: a)
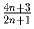 b)
b) 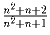 .
.Задача 17: a) Найти наименьший общий делитель (НОД) (11 … 1 (9 единиц), 11 … 1 (6 единиц)).
b) Доказать, что наименьший общий делитель числа из a единиц и числа из b единиц равен числу из НОД(a,b) единиц.
Задача 18: a) Разделить с остатком 2²¹ – 1 на 2¹³ – 1.
b) Найти НОД этих чисел.
Задача 19: Доказать, что для любого n > 2 найдется простое число между n и n!.
Задача 20: Доказать, что
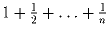 не целое.
Задача 21:
a + b = 239, a, b – натуральные числа. Чему может быть
равен НОД(a,b)?
не целое.
Задача 21:
a + b = 239, a, b – натуральные числа. Чему может быть
равен НОД(a,b)?Задача 22: n < 106. Доказать, что количество делителей n меньше 2000.
Задача 23: d(n) – количество делителей числа n. Доказать, что их произведение равно
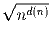 .
.Задача 24: На что можно сократить дробь
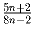 и при каких n ?
и при каких n ?Задача 25: Доказать, что максимальная степень p, на которую делится n!, равна
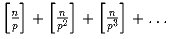 , p – простое число.
, p – простое число.Задача 26: Найти все четные a, обладающие следующим свойством: если a делится на простое p, то a – 1 делится на p – 1.
Задача 27: Дробь
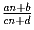 сократима на k. Доказать, что ad – bk делится на
k.
Задача 28:
a1, … ,an – различные натуральные числа, a1 – наименьшее из
них. Доказать, что НОК(a1, … ,an) ≥ na1.
сократима на k. Доказать, что ad – bk делится на
k.
Задача 28:
a1, … ,an – различные натуральные числа, a1 – наименьшее из
них. Доказать, что НОК(a1, … ,an) ≥ na1.Задача 29: Найти все натуральные числа делящиеся на 18 и имеющие ровно a) 17 b) 14 c) 15 делителей.
Задача 30: Число n имеет ровно 1982 делителя. Доказать, что n не делится на 66.
Задача 31: Число
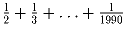 записано в виде несократимой дроби
записано в виде несократимой дроби
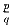 . На сколько нулей оканчивается q?
. На сколько нулей оканчивается q?Задача 32: a, b – натуральные числа, a + b = 30030. Доказать, что ab не делится на 30030.
Задача 33: Доказать, что n! делится на 2n.
Задача 34: Найти наименьшее натуральное число, являющееся одновременно удвоенным квадратом, утроенным кубом и умноженной на 5 пятой степенью натурального числа.
Задача 35: Доказать, что (n + 1)(n + 2) … (2n – 1)2n делится на n!.
Проще всего воспользоваться комбинаторными соображениями.
Задача 36: Число A равно (16a + 17b)(17a + 16b), где a и b – целые. Известно, что A делится на 11. Доказать, что A делится на 121.
| Задачная база >> Разное >> Задачник первого-второго года обучения >> Делимость | Показать решения |