 |
 |
|
| Задачная база >> Разное >> Задачник первого-второго года обучения >> Геометрия | Показать решения |
|
|
| Математический кружок. Задачник первого-второго года обучения. Геометрия |
|
|
a) В равнобедренном треугольнике углы при основании равны.
b) Если два угла у треугольника равны, то он равнобедренный.
Задача 2: Доказать, что
a) В равнобедренном треугольнике медиана, биссектриса и высота совпадают.
b) Если биссектриса совпадает с высотой, то треугольник равнобедренный.
c) То же, если медиана и биссектриса совпадает.
d) То же, если высота совпадает с медианой.
Задача 3: Доказать, что биссектрисы соседних углов параллелограмма перпендикулярны.
Задача 4:
a) Найти сумму углов выпуклого n-угольника.
b) Каково максимально возможное количество острых углов в нем?
Задача 5: Доказать, что в треугольнике напротив большего угла лежит большая сторона.
Задача 6: Доказать, что в прямоугольном треугольнике медиана с основанием на гипотенузе равна половине гипотенузы.
Задача 7: Найти сумму углов a) пятиугольной звезды; b) семиугольной звезды.
Задача 8: Доказать, что в прямоугольном треугольнике биссектриса прямого угла проходит через центр квадрата, построенного на гипотенузе во внешнюю сторону.
Задача 9: Доказать, что равнобедренная трапеция – вписанный четырехугольник.
Задача 10: ABCD – квадрат, O – точка внутри него, такая, что ∠ OAD = ∠ ODA = 15 . Доказать, что треугольник BOC – равносторонний.
Задача 11: Две окружности пересекаются в точках A и B. A1 и A2 – точки, диаметрально противоположные A на первой и второй окружности. Доказать, что A1, B и A2 лежат на одной прямой.
Задача 12: Доказать, что средняя линия треугольника параллельна основанию и вдвое меньше его по длине.
Задача 13: Доказать, что биссектриса – это геометрическое место точек, равноудаленных от сторон угла.
Задача 14: Доказать, что углы при основании равнобочной трапеции равны.
Задача 15: Выразить угол между двумя биссектрисами через углы треугольника.
Задача 16: Выразить угол между двумя внешними биссектрисами через углы треугольника.
Задача 17: ha и hb – высоты треугольника, опущенные на стороны a и b. Известно, что ha ≥ a, hb ≥ b. Найти углы треугольника.
Задача 18: Дана трапеция с основаниями a и b, a ≥ b,
a) Доказать, что длина средней линии равна 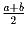 .
.
b) Доказать, что длина отрезка средней линии между
диагоналями равна 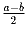 .
.
Задача 19: Дан угол и точка внутри него. Найти точки X и Y на сторонах угла такие, что A – середина отрезка XY.
Задача 20:
a) Доказать признак равенства треугольников по двум сторонам и медиане между ними.
b) Верен ли такой же признак равенства по двум сторонам и высоте?
Задача 21: ABCD – выпуклый четырехугольник. Доказать, что ∠ A + ∠ B ≥ ∠ C – ∠ D.
Задача 22: Доказать, что a) если две высоты треугольника равны, то он равнобедренный. b) если две медианы треугольника равны, то он равнобедренный.
Задача 23: В треугольнике ABC AB > BC. На продолжении стороны отложен отрезок BD, равный AB. Доказать, что ∠ ACD > 90 .
Задача 24: Существует ли правильный n-угольник, у которого одна диагональ равна сумме двух других?
Задача 25: Доказать, что a) если в параллелограмме диагонали перпендикулярны, то он – ромб. b) если диагонали равны, то он – прямоугольник.
Задача 26: В трапеции одна из диагоналей делится другой пополам. Доказать, что эта трапеция является параллелограммом.
Задача 27: Доказать, что середины сторон четырехугольника образуют параллелограмм.
Задача 28: Доказать, что диагонали четырехугольника перпендикулярны тогда и только тогда, когда средние линии равны.
Задача 29: Доказать, что диагонали четырехугольника равны тогда и только тогда, когда средние линии перпендикулярны.
Задача 30: Доказать, что точка пересечения двух медиан в треугольнике делит каждую из них в отношении 2:1.
Задача 31: Доказать, что три медианы треугольника пересекаются в одной точке.
Задача 32: ABCD – параллелограмм, O – точка пересечения его диагоналей. Доказать, что SOAB + SOCD = SOAD + SOBC.
Задача 33: Доказать, что радиус вписанной окружности треугольника равен
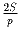 (S – площадь, P – периметр).
(S – площадь, P – периметр).Задача 34: Четыре прямоугольных треугольника с катетами a, b и гипотенузой c уложены в квадрат со стороной c.
a) Найти площадь среднего квадратика.
b) Доказать теорему Пифагора: c² = a² + b².
Задача 35: Доказать, что любой четырехугольник покрывается кругами, построенными на его сторонах как на диаметрах.
Задача 36: Дан выпуклый четырехугольник. 4 треугольника, на которые он разбивается диагоналями, имеют равные площади. Доказать, что четырехугольник является параллелограммом. Задача 38: ABCD – трапеция, O – точка пересечения ее диагоналей. Доказать, что SAOB + SCOD = SAOD + SBOC.
Задача 39: r – радиус вписанной окружности треугольника, ha, hb, hc - высоты. Доказать, что
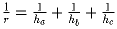 .
.Задача 40: a) В выпуклом четырехугольнике провели две среднии линии, и получившиеся 4 четырехугольника раскрасили в шахматном порядке. Доказать, что сумма площадей белых частей равна сумме площадей черных.
b) Доказать тоже самое для картинки , где каждая сторона разбита на 4 равные части, и точки деления соединены с соответствующими на противоположной стороне четырехугольника.
Задача 41: a) ABCD – выпуклый четырехугольник, X – середина CD. Доказать, что SABX = ½(SABC + SABD).
b) ABCD – выпуклый четырехугольник, M – середина AB, N – середина BC. SABCD = 1. Найти SABC + SDMC + SAND.
Задача 42: Доказать, что угол, вписанный в окружность и опирающийся на диаметр, прямой.
Задача 43: Доказать, что угол, вписанный в окружность, равен половине стягиваемой им дуги.
Задача 44: a) Доказать, что у вписанного четырехугольника сумма противоположных углов равна 180 градусов.
b) Доказать обратное утверждение.
Задача 45: На середине прислоненной к стене лестницы сидит кошка. Лестница начинает съезжать. Какую линию опишет кошка?
Задача 46: Угол с вершиной вне окружности высекает на ней дуги с величинами a и b. Доказать, что величина угла равна
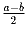 (если
a > b).
(если
a > b).Задача 47: Угол с вершиной внутри окружности высекает на ней дуги с величинами a и b. Доказать, что его величина равна
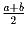 .
.Задача 48: Доказать, что дуги, высекаемые на окружности парой параллельных прямых, равны:
a) если обе прямые пересекают окружность в двух точках
b) если одна из них является касательной.
Задача 49: Даны две пересекающиеся окружности. ABCD – выпуклый четырехугольник, причем A и D лежат на одной окружности, B и C - на другой, стороны AB и CD проходят через точки пересечения окружностей. Известно, что ABCD – вписанный. Доказать, что AD параллельно BC.
Задача 50: ABCD – квадрат, E – середина стороны AD, k – точка по диагонали AC, такая, что AK:KC = 3:1. Доказать, что угол BKE – прямой.
Задача 51: Выразить через стороны треугольника длины отрезков между вершинами и точками касания вписанной окружности.
Задача 52: Из точки A вне окружности проведена касательная AD и секущая, пересекающая окружность в точках B и C. Доказать, что a) треугольники ABD и ADC подобны b) AB • AC = AD².
Задача 53: ABC – произвольный треугольник. Проведена вневписанная окружность, касающаяся стороны BC и продолжений сторон AB и AC.B1 – точка касания этой окружности и продолжения стороны AB.
a) Доказать: 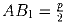 (p – периметр треугольника).
(p – периметр треугольника).
b) Доказать, что 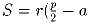 ). (r – радиус окружности).
). (r – радиус окружности).
Задача 54: ABCD – выпуклый четырехугольник. E – середина AB,F – середина CD. Точки A1, A2, A3, A4 лежат на стороне AD (и перечислены в порядке удаления от A), для ее на 5 равных отрезков. Аналогично определяются точки B1, B2, B3, B4 на стороне BC. Доказать, что EF делится на 5 равных частей точками пересечения с отрезком AiBi.
Задача 55: Отрезки AD и BC пересекаются в точке X, причем AX = DX = BD. Y – такая точка на отрезке BC, что BX = CY. Доказать, что AC = DY.
Задача 56: a) Доказать, что биссектрисы углов треугольника пересекаются в одной точке.
b) Доказать, что серединные перпендикуляры сторон пересекаются в одной точке.
Задача 57: В выпуклом четырехугольнике ABCD угол B – прямой. Диагональ AC является биссектрисой угла, и по длине равна стороне AD. X – основание перпендикуляра, опущенного из D на AC. Прямая BX пересекает CD в точке Y. Доказать, что Y – середина CD.
Задача 58: a, b, c – стороны треугольника (сторона c лежит напротив угла C). Доказать, что:
если 2C = 90 , то c² = a² + b²
если 2C = 90 , то c² > a² + b²
если 2C = 90 , то c² < a² + b².
Задача 59: С помощью циркуля и линейки разделить отрезок на a) 3 b) 5 равных частей.
Задача 60: Даны отрезки длины 1, a, b. С помощью циркуля и линейки построить отрезки ab и a/b.
Задача 61: Провести окружность, вписанную в данный угол и проходящую через данную точку.
Задача 62: Выразите высоту прямоугольного треугольника, опущенную на гипотенузу, через катеты.
Задача 63: Выразить высоту треугольника через стороны.
Задача 64: a) Дана окружность радиуса r и точка x внутри окружности, AB – хорда, проходящая через точку x. Доказать, что AX • BX = r² – OX².
b) Дана окружность радиуса r и точка X вне окружности. AB - хорда, продолжение которой проходит через X. Доказать, что AX • BX = OX² – r².
Задача 65: Доказать, что для выпуклого четырехугольника ABCD следующие условия эквивалентны:
1. B, C, D лежат на окружности с центром A.
2. Серединные перпендикуляры к BC и CD проходят через A.
3. AB = CD и ∠ A + 2 ∠ C = 360 .
Задача 66: В трапеции ABCD (с основанием AD) биссектриссы углов A и B пересекаются в точке M, биссектриссы углов C и D – в точке N. Доказать, что MN = AD + BC – AB – CD.
Задача 67: С помощью циркуля и линейки восстановить параллелограмм ABCD по вершине A и серединам сторон BC и CD.
Задача 68: Высоты треугольника ABC пересекаются в точке O, причем OC = AB. Найти угол при вершине C.
Задача 69: Окружность, построенная на катете прямоугольного треугольника, как на диаметре, делит гипотенузу в отношении 1:3. Найти углы треугольника.
| Задачная база >> Разное >> Задачник первого-второго года обучения >> Геометрия | Показать решения |