 |
 |
|
| Задачная база >> Разное >> Задачник первого-второго года обучения >> Инвариант | Убрать решения |
|
|
| Математический кружок. Задачник первого-второго года обучения. Инвариант |
|
|
Задача 2: a) Хулиган Вася порвал стенгазету, причем каждый попадающийся ему кусок он рвал на четыре части. Могло ли получиться 1989 кусков?
b) А если каждый кусок рвался на 4 или 10 частей?
Решение: Нет. Количество кусков должно иметь остаток 1 по модулю 3. Задача 3: В клетках таблицы 3 × 3 стоят нули. Можно прибавлять по 1 к клеткам любого квадрата 2 × 2. Можно ли получить таблицу?
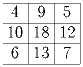
Задача 4: В одной вершине куба написано число 1, в остальных – нули. Можно прибавлять по единице к числам в концах любого ребра. Можно ли добиться, чтобы все числа
a) делились на 2
b) делились на 3.
Решение: b) Раскрасим вершины в шахматном порядке. После этого сумма чисел в белых вершинах всегда будет отличаться на 1 от суммы чисел в в чёрных вершинах, так как и к тем и к другим прибавляется по единице. Задача 5: В углу квадрата a) 4 × 4 b) 3 × 3 стоит минус, в остальных – плюсы. Можно ли заменять все знаки в любом столбце или строке на противоположные. Можно ли получить таблицу из одних плюсов?
Решение: Количество минусов в угловом квадрате 2 × 2 всегда будет нечётно.
Задача 6: Круг разделили на 6 секторов, в каждом лежит селедка. За ход можно одну селедку передвинуть в соседний сектор. Можно ли собрать все селедки в одном секторе ровно за 20 ходов?
Решение: Нет. Указание: раскрасьте сектора в шахматном порядке. Задача 7: В ряд выписаны числа 1, 2, 3,…,100. Можно менять местами любые два числа, между которыми стоит ровно одно. Можно ли получить ряд 100, 99, 98,…, 2, 1?
Задача 8: К числу можно прибавлять сумму его цифр. Можно ли за несколько шагов получить из единицы число 123456?
Задача 9: На доске выписаны числа от 1 до 21. Можно любые два числа заменять на модуль их разности. Может ли в конце (после 20 операций) остаться 0?
Задача 10: На столе стоят 50 стаканов, из них 25 – вверх дном. Можно ли, переворачивая по 4 стакана, получить все стаканы стоящими правильно?
Задача 11: a) Можно ли операциями «прибавить 4» и «умножить на 3» получить из единицы число 1990?
b) Какие числа можно получить?
Решение: b) Все нечётные числа. Задача 12: На доске написано 100 плюсов и 100 минусов. Можно заменять любые 2 минуса на плюс, плюс и минус на минус, два плюса на плюс. Доказать, что знак, который останется в конце, не зависит от порядка операций.
Задача 13: Круг разделен на 6 секторов, в которых по часовой стрелке стоят числа a) 1,0,0,0,0,0 b) 1,0,1,0,0,0. Можно прибавлять по единице к любым двум соседним секторам. Можно ли сделать все числа равными?
Решение: b) Нет. Указание: раскрасьте сектора в шахматном порядке. Задача 14: На доске написаны числа от 1 до 20. Можно любую пару чисел x, y заменять на x + y + 5xy. Может ли в конце получиться 19901989?
Решение: Нет. Сумма всех чисел всегда будет делиться на 5.
Задача 15: Фигура ходит по диагонали прямоугольника 1 × n (например, для коня это 1 × 2). При каком n она может попасть с любой клетки на любую на бесконечной доске?
Решение: При чётных n Задача 16: На доске написаны числа от 1 до 20.
a) Можно пару чисел (x, y) заменить на x + y. Какое число останется после 19 таких операций?
b) Можно (x, y) заменить на 3x + 5y. Может ли в конце остаться 45239?
c) (x,y) можно заменить на 4(x + y). Может ли в конце остаться 4000?
Задача 17: Квадрат a) 2 × 2 b) 3 × 3 заполнен плюсами. Можно в любой строке или в любом столбце менять все плюсы на минусы. Сколько различных расстановок плюсов и минусов можно получить такими операциями?
Решение: а) 8; б) 32
Задача 18: На доске написаны числа от 1 до 20. Можно пару чисел (x,y) заменить на x + y + xy. Какое число останется после 19 операций?
Решение: 21! – 1. Указание: прибавьте ко всем числам по единице. Задача 19: В шести секторах круга лежат по селедке. Можно одновременно передвинуть две селедки в соседних секторах, двигая их в противоположных направлениях. Можно ли получить расположение
a)6, 0, 0, 0, 0, 0. b) 5, 1, 0, 0, 0, 0.
Решение: b) Пронумеруем сектора числами от 1 до 6 по часовой стрелке и напишем на каждой селёдке номер её сектора. Сумма написанных чисел всегда будет делиться на 3.
Задача 20: В квадрате 10 × 10 стоят 100 ненулевых чисел. Можно менять знак у чисел в любом столбце или строке.
a) Всегда ли можно сделать все числа положительными?
b) Всегда ли можно сумму в любом столбце или в любой строке сделать неотрицательной?
Решение: а) Нет. b) Да. Задача 21: По окружности стоят 3 числа. На каждом шагу между каждыми двумя пишут модуль их разности, а старые числа стирают. Могут ли через 100 шагов получиться числа a) 60, 70, 150. b) 60, 70, 130.
Решение: а) Нет. b) Да.
Задача 22: На доске написаны числа 2, 2, 2. Числа a,b,c можно заменять на a,b,a + b – 1.
a) Можно ли такими операциями получить набор 19,1971,1989.
b) Какие наборы можно получить?
Решение: Указание: следите за чётностью. Задача 23: a) Набор из трех чисел a,b,c каждую секунду заменяется на набор a + b – c,a + c – b,b + c – a. В начале имеется набор из чисел 1989, 1990, 1991. Может ли через некоторое время получиться набор 1987, 1990, 1991?
b) Тот же вопрос, если числа a,b,c заменяются на 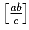 ,
,
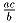 ,
, 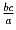 .
.
Задача 24: Квадрат 4 × 4 раскрашен в 2 цвета. Можно менять цвет у всех клеток любого столбца или строки. Характеристикой раскраски называется наименьшее число черных клеток, которого можно достичь такими операциями.
a) Доказать, что бывают раскраски с характеристиками 0, 1, 2, 3, 4.
b) Какие характеристики бывают?
Задача 25: На доске написаны числа от 1 до 1990. Можно любую пару чисел a, b заменить на число a² – b². Можно ли добиться, чтобы в конце (после 1989 операций) остался ноль?
Задача 26: a) В квадрате 4 × 4 клетка, соседняя с угловой, – черная, а остальные – белые. Можно перекрашивать все клетки любого столбца, строки или диагонали (не обязательно главной). Доказать, что такими операциями нельзя получить целиком белый квадрат.
b) То же для квадрата 8 × 8, у которого закрашена любая не угловая клетка.
Задача 27: В квадрате 8 × 8 стоят целые числа. Можно прибавлять по единице ко всем числам любого квадрата 3 × 3 или 4 × 4. Всегда ли можно добиться, чтобы все числа в таблице делились на 3?
Решение: Нет. Первый способ: заменим все числа в таблице а их остатки по модулю 3. Тогда количество различных таблиц, которые можно получить из нулевой, не больше 361, а всего таблиц – 364.
Второй способ: найдите две группы клеток, суммы чисел в которых (по модулю 3) меняются одинаково.
Задача 28: a) В ряд стоят несколько фишек. Можно менять местами любые две соседние. После нескольких таких операций обнаружили, что все фишки оказались на своих исходных местах. Доказать, что было сделано четное число перестановок.b) То же, если менять местами можно любые две (не обязательно соседние) фишки.
Решение: б) Такой обмен можно реализовать нечётным числом операций из пункта а). Задача 29: На доске написаны три числа. можно брать любые два из них – a и b и заменять их на
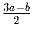 ,
, 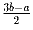 .
В начале написаны числа
1990, 1995, 1996. Можно ли получить набор 1991, 1994, 1997?
.
В начале написаны числа
1990, 1995, 1996. Можно ли получить набор 1991, 1994, 1997?Задача 30: В ряд выписаны числа от 1 до 1991. Разрешается брать любые 4 числа и переставлять их в обратном порядке. Можно ли такими операциями получить ряд 1991, 1990, …, 2, 1?
Задача 31: В городе разрешены только тройные обмены квартир. Можно ли с помощью них осуществить обычный (двойной) обмен?
Задача 32: Автомат работает с карточками, на которых написаны пары чисел. Из карточки (a,b) он может сделать (a/2, b/2), если a и b четны, или (a + 1,b + 1). Из карточки (a,b) и (b,c) он может сделать карточку (a,c). Исходные карточки он возвращает. Вначале есть карточка (5,10).
a) Можно ли получить (1,100)?
b) Можно ли получить (1,50)?
c) Для каких x можно получить карточку (1,x)?
Решение: c) Для всех x вида 7k + 1, где k – натуральное число. Задача 33: Три кузнечика сидят на плоскости в точках с координатами (0,0), (0,1), (1,0). Каждую секунду один из них прыгает в точку симметричную относительно какого-то другого.
a) Могут ли они попасть в точки (0,1), (1,0), (1,1)?
b) В точки (x,y), (x + 1,y + 1), (x + z,y)?
c) Могут ли они попасть в точки (x,y), (x + 3,y), (x,y + 3)?
Решение: a) и b). Проследите за чётностью координат. с) Площадь треугольника, образованного кузнечиками, сохраняется. Задача 34: 4 кузнечика играют в чехарду на плоскости, как в предыдущей задаче. Вначале они находятся в точках (0,0), (0,1), (1,1). Могут ли они попасть в точки (x,y), (x + 1,y + 1), (x + 3,y), (x + 2,y – 1)?
Решение: Запустите процесс в обратном направлении Задача 35: В алфавите имеются только две буквы – А и Я. Комбинации букв АЯ и ЯЯЯ, ЯА и ААЯ, ЯЯ и ААА в любом слове можно заменять друг на друга. Можно ли из слова АЯЯ получить слово ЯАА?
Задача 36: Написаны 4 числа: a,b,c,d. Каждую секунду они заменяются на числа a + b,b + c,c + d,d + a. Через некоторое время опять получились исходные числа. Доказать, что все числа равны нулю.
Задача 37: 239 машин целый день ездили по круговой дороге в одном направлении. Вечером все они оказались на тех же местах, откуда начинали. Доказать, что они совершили четное число обгонов.
Решение: Разрежем дорогу в произвольном месте, и тогда машины образуют некоторую перестановку. Легко проверить, что её чётность совпадает с чётностью числа обгонов.
| Задачная база >> Разное >> Задачник первого-второго года обучения >> Инвариант | Убрать решения |