Задача 1: Сколько квадратов со сторонами по линиям сетки можно нарисовать на доске 8 × 8?

Задача 2: Сколько способов расставить n человек в ряд?

Задача 3: Сколько способов выбрать a) двух человек из десяти?

b) трех человек из десяти?

c) k человек из n?

(Ответ: это число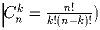

Задача 4: Доказать, что .

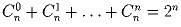Задача 5: Сколько способов сделать бусы из a) семи разных бусинок b) пяти белых и двух черных бусинок (Бусы – это окружность, на которую насажены бусины. Ее можно поворачивать, но нельзя переворачивать).

Задача 6: Доказать, что 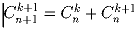a) по формуле b) с помощью комбинаторных рассуждений.

Задача 7: Доказать, что .

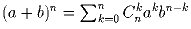Задача 8: Сколько способов расставить на полку 3 книги одного вида, 5 – другого и 8 – третьего?

Задача 9: p – простое число. Доказать, что 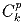делится на p.

Задача 10: Сколько способов разбить 12 человек на две группы по 12 и 5 человек так, чтобы:

a) два данных человека оказались в разных группах.

b) в одной группе?

Задача 11: a) Доказать, что число способов выбрать k человек из n и выбрать из них главного равно .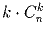

b) Доказать, что то же самое число равно .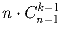

Задача 12: Сколько способов расставить 20 разных книг по 5 полкам?

Задача 13: Сколько способов расставить 25 разных книг по 5 полкам так, чтобы на каждой было не менее одной книги?

Задача 14: Сколько способов расставить 25 одинаковых книг по 5 полкам (некоторые полки могут оказаться пустыми)?

Задача 15: Сколько способов расставить на доске 8 × 8 a) 8 ладей b) 32 коня так, чтобы они не били друг друга?

Задача 16: Сколько всего 6-значных чисел

a) без единиц в записи.

b) по крайней мере с одной единицей в записи.

Задача 17: Сколько существует семизначных чисел, у которых

a) все цифры разные

b) любые две соседних цифры разные

c) есть две одинаковых цифры.

Задача 18: Сколько способов рассадить 5 мужчин и 5 женщин за круглым столом так, чтобы мужчины и женщины чередовались?

Задача 19: В классе 30 человек. Сколько способов разбить класс на две группы и в каждой выбрать старосту?

Задача 20: Сколько 7-значных чисел, в которых

a) каждая цифра больше предыдущей?

b) каждая цифра не меньше предыдущей?

Задача 21: Сколько способов разбить 15 мужчин и 15 женщин на пары для танцев?

Задача 22: Сколько разных слов можно составить из слова:

a) ПЕРЕЕЗД b) МАТЕМАТИКА c) АА … АББ … ББ (n букв «А», m букв «Б")

Задача 23: Доказать тождества:

a) .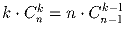

b) .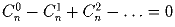

c) .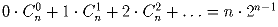

Задача 24: Сколько способов прочитать слово "ТРЕУГОЛЬНИК", двигаясь вправо и вниз:

а)

б)

Задача 25: a) Круг разбит на простое число p секторов. Сколько способов раскрасить их в n цветов (раскраски, совмещающиеся при повороте, считаются одинаковыми).

b) Вывести из пункта a) малую теорему Ферма: n^p – n делится на p.

Задача 26: a,b – натуральные числа, a ≥ b – 1. Сколько способов расставить a белых и b черных фишек так, чтобы черные не стояли рядом?

Задача 27: Доказать, что .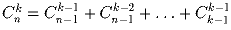

Задача 28: Пусть p – простое число. Доказать, что:

a) если k не делится на p, то 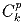делится на p;

b) (a + b)^p ≡ a^p + b^p (mod %)%p;

c) (a + b +  …  + d)^p ≡ a^p + b^p +  …  + d^p (mod %)%p.

d) Вывести из пункта c) малую теорему Ферма: a^p ≡ a (mod %)%p.

Задача 29: На окружности отмечено 11 точек.

a) Сколько существует многоугольников с вершинами в отмеченных точках?

b) Каких из них больше: содержащих данную отмеченную точку или остальных?

Задача 30: Сколько способов выбрать:

a) 3 пары из 100 человек?

b) n пар из 2n человек?

Задача 31: Каких 6-значных чисел больше: представляющихся в виде произведения двух трехзначных или остальных?

Задача 32: На дороге длиной 999 километров стоят 1000 километровых столбов, на каждом из которых написаны два числа – расстояние до начала и до конца дороги. Сколько среди этих столбов таких, на которых числа записаны только двумя различными цифрами?