 |
 |
|
| Задачная база >> Разное >> Задачник первого-второго года обучения >> Разные задачи | Показать решения |
|
|
| Математический кружок. Задачник первого-второго года обучения. Разные задачи |
|
|
Задача 3: Есть два стакана: один с молоком, другой с водой.
a) Из первого перелили ложку во второй, перемешали и перелили ложку смеси обратно. Чего больше: воды в стакане с молоком или молока в стакане с водой?
b) Тот же вопрос, если описанную процедуру повторили 100 раз.
Задача 4: В комнате стоят несколько четырехногих стульев и трехногих табуреток. Когда на всех стульях и табуретках сидит по человеку, в комнате всего 39 ног. Сколько в комнате стульев и сколько табуреток? Задача 5: В кружке есть девочки, но мальчиков больше 94 состава. Какое минимальное число людей может быть в кружке? Задача 6: В двух стаканах было поровну воды. Количество воды в первом увеличилось вначале на 1, потом на 2, потом на 3, и так далее до 27. Во втором стакане количество воды увеличилось вначале на 27, потом на 26, потом на 25 и так далее до 1. В каком стакане стало больше воды?Задача 7: Из ста человек 85 – без уха, 75 – без глаза. Какое наименьшее возможное число полных инвалидов?
Задача 8: В партии из 300 сапог 150 левых и 150 правых, кроме того, по 100 штук каждого из трех размеров. Доказать, что есть по крайней мере 50 годных пар.
Задача 9: В автобусе едут 20 пассажиров, и у каждого много монет по 10, 15 и 20 копеек. Каждый должен заплатить 5 копеек. Могут ли они сделать это, использовав (в том числе и для обмена межу собой)a)24 монеты b)25 монет? Задача 10: Лифт в 100-этажном доме имеет 2 кнопки: « + 7» и «-9». (первая поднимает лифт на 7 этажей, вторая опускает на 9).Можно ли проехать:
a) с первого на второй;
b) со второго на первый;
c) с любого на любой этаж?
Задача 11: В 15-этажном доме имеется лифт с двумя кнопками: « + 7" и « – 9". Можно ли проехать с третьего этажа на двенадцатый ?
Задача 12: Как с помощью наименьшего числа прямолинейных разрезов разрезать квадрат 3 × 3 на единичные квадраты
a) если части нельзя накладывать (т.е. каждый раз можно разрезать только одну часть)
b) если части можно накладывать.
c) если перед разрезами квадрат можно сложить? (Ответ: достаточно одного разреза)
Задача 13: Как разрезать на единичные квадраты квадрат a)4 × 4 b) 5 × 5 за наименьшее число разрезов. (Части при разрезании можно накладывать друг на друга). Задача 14: Расставьте в ряд числа от 1 до 100 так, чтобы любые два соседних отличались по крайней мере на 50. Задача 15: 50 команд сыграли турнир по волейболу в один круг. Говорят, что команда А сильнее В, если А выиграла у В или есть команда С, такая, что А выиграла у С, а С выиграла у В.Доказать, что команда, набравшая наибольшее число очков, сильнее любой другой.Задача 16: 30 команд сыграли турнир по олимпийской системе. Сколько всего было сыграно матчей? Задача 17: Квадрат 8 × 8 раскрашен в два цвета. Можно любой прямоугольник 1 × 3 перекрашивать в преобладающий в нем цвет. Доказать, что такими операциями можно сделать весь квадрат одноцветным.
Задача 18: Некто А загадал число от 1 до 15. Некто В задает вопросы на которые можно отвечать «да" или «нет". Может ли В отгадать число, задав a)4 вопроса b)3 вопроса.
Задача 19: a) В группе из четырех человек, говорящих на разных языках, любые трое могут общаться (возможно, один переводит двум другим). Доказать, что их можно разбить на пары, в каждой из которых имеется общий язык.
b) То же для группы из 100 человек.
c) То же для группы из 102 человек.
Задача 20: 12 команд сыграли турнир по волейболу в один круг. Две команды одержали ровно по 7 побед. Доказать, что найдутся команды А, В, С такие, что А выиграла у В, В выиграла у С, а С – у А. Задача 21: Когда встречаются два жителя Цветочного города, один отдает другому монету в 10 копеек, а тот ему – 2 монеты по 5 копеек. Могло ли случиться так, что за день каждый из 1990 жителей города отдал ровно 10 монет? Задача 22: Матч между двумя футбольными командами закончился со счетом 8:5. Доказать, что был момент, когда первая команда забила столько же мячей, сколько второй оставалось забить.
Задача 23: В центре куба 3 × 3 × 3 сидит жук. Доказать, что он, переползая через ребра, не сможет обойти все кубики 1 × 1 × 1 по одному разу. Задача 24: В ряд выписаны числа от 1 до 9999. Как вычеркнуть из этой записи 100 цифр так, чтобы оставшееся число было a) максимальным b) минимальным?
Задача 25: В прямоугольнике 3 × n стоят фишки трех цветов, по n штук каждого цвета. Доказать, что можно переставить фишки в каждой строке так, чтобы в любом столбце были фишки всех цветов.
Задача 26: К числу 2¹ºº приписано число 5¹ºº. Сколько цифр написано?
Задача 27: Сколько решений в натуральных числах имеет уравнение
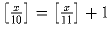 ?
?Задача 28: Имеется бесконечная арифметическая прогрессия с натуральными членами. Доказать, что найдется член, в котором есть 100 девяток подряд.
Задача 29: 12 шахматистов сыграли турнир в один круг. Потом каждый из них написал 12 списков. В первом только он, в (k + 1)-м – те, кто были в k-м и те, у кого они выиграли. Оказалось, что у любого шахматиста 12-й список отличается от 11-го. Сколько было ничьих?
Задача 30: В городе 100 домов. Какое наибольшее число замкнутых непересекающихся заборов можно построить так, чтобы любые 2 забора ограничивали разные группы домов? Задача 31: Несколько человек стоят прямоугольником. В каждой шеренге выбрали самого нижнего, в каждом ряду самого высокого. Кто выше: самый низкий из высоких или самый высокий из низких?
Задача 32: Несколько человек построились в два ряда. Каждый во втором ряду выше стоящего перед ним. Доказать, что если каждый ряд построить по росту, то это свойство сохранится.
Задача 33: Имеются две одинаковых шестеренки по 14 зубьев на общей оси. Их совместили и выбили 4 пары зубьев. Доказать, что шестеренки можно повернуть так, что они образуют полноценную шестеренку (без дырок).
Задача 34: Фигура может ходить вправо, вниз и по диагонали «вверх"-«влево". Может ли она обойти прямоугольную доску и вернуться? Задача 35: На круглом столе лежат 12 табличек с именами. 12 человек, имена которых написаны на табличках, сели за стол как попало. Доказать, что можно повернуть стол так, что по крайней мере двое оказались рядом со своей табличкой. Задача 36: В ста домах жили 100 гномов. Однажды некоторые из них (возможно, все) переехали так, что расстояние между любыми двумя гномами не уменьшилось. Доказать, что все эти расстояния остались прежними.
Задача 37: В прямоугольной таблице стоят натуральные числа. Разрешается вычетать единицу из всех чисел любого столбца и умножать на два все числа в любой строке. Доказать, что можно получить таблицу из одних нулей.
Задача 38: Автомат разменивает любую монету, кроме 1коп. и 2коп., на 3 монеты (бывают монеты по 1, 2, 3, 5, 10, 15, 20 и 50 коп.). Способ размена фиксирован. Вначале имеется монета 50 коп.
a) Можно ли ее разменять на 20 монет?
b) Всегда ли можно получить 23, 25, 27 монет?
c) Всегда ли можно получить 29 монет?
d) Доказать, что можно так задать способ размена, что 50коп. можно будет разменять на 49 монет.
e) Какое максимальное число монет заведомо можно получить (независимо от устройства автомата)?
Задача 39: Плоскость разбита на правильные треугольники со стороной 1. По границам этих треугольников проведена замкнутая ломанная, все углы которой равны 60 . Доказать, что длина этой ломаной делится на 3.
Задача 40: Доказать, что из чисел 0,1,2, … ,3k – 1 можно выбрать 2k чисел, никакое из которых не равно полусумме двух других.
Задача 41: Двадцать команд сыграли однокруговой турнир по волейболу. Bi – число выигрышей i-й командой, Пi – число проигрышей. Доказать, что
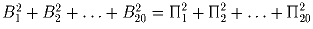 .
.Задача 42: Квадрат 8 × 8 замощен доминошками. Доказать, что найдутся две соседние доминошки, образующие квадрат 2 × 2.
Задача 43: Имеется набор гирь, вес каждой из которых не больше 100 грамм. Известно, что гири нельзя разбить на две группы, каждая из которых весит больше 100 грамм. Какой максимальный суммарный вес такого набора?
Задача 44: В клетках бесконечной плоскости записаны натуральные числа без повторений. Доказать, что есть две соседние клетки, числа в которых отличаются больше, чем на миллион.
Задача 45: На столе лежат 15 тетрадей в нескольких стопках. С ними повторяют следующую операцию: берут из каждой стопке по тетради и составляют из них новую стопку. Доказать, что когда-нибудь окажется 5 стопок, в которых будут 1, 2, 3, 4 и 5 тетрадей. Задача 46: В ряд лежат 20 монет: орел, решка, орел, решка, и т.д.. Можно одновременно переворачивать несколько подряд. За какое наименьшее число операций можно перевернуть все монеты орлами вверх? Задача 47: Число x заменили на x² – 600, с полученным числом снова проделали такую операцию и так 100 раз. Получилось опять число x. Найти x. Задача 48: В парламенте у каждого члена не больше трех врагов. Доказать, что его можно разбить на две палаты так, что у каждого будет не больше одного врага в своей палате. Задача 49: В каждой клетке бесконечной плоскости стоит натуральное число, равное среднему арифметическому соседей. Доказать, что все числа равны. Задача 50: В таблице 7 × 7 в клетках стоят плюсы и минусы. Можно одновременно менять знаки в любом столбце или строке. Доказать, что можно сделать так, чтобы в любом столбце и в любой строке плюсов было больше, чем минусов. Задача 51: На плоскости лежит правильный треугольник. Его «катают», переворачивая через сторону. Через несколько шагов он вернулся на исходное место. Доказать, что
a) Он сделал четное число переворотов.
b) Все вершины вернулись на свои места.
| Задачная база >> Разное >> Задачник первого-второго года обучения >> Разные задачи | Показать решения |