 |
 |
|
| Задачная база >> Разное >> Математический кружок. 1-й год >> Делимость и остатки >> Остатки | Показать решения |
|
|
| С.А.Генкин, И.В.Итенберг, Д.В.Фомин. Математический кружок. Делимость и остатки. Остатки |
|
|
Найдите остатки от деления
а) 1989 • 1990 • 1991 + 1992³ на 7;
б) 9¹ºº на 8.
Задача 16:
Докажите, что n³ + 2n делится на 3 для любого натурального n.
Задача 17:
Докажите, что n5 + 4n делится на 5 при любом натуральном n.
Задача 18:
Докажите, что n² + 1 не делится на 3 ни при каком натуральном n.
Задача 19:Докажите, что n³ + 2 не делится на 9 ни при каком натуральном n.
Задача 20:Докажите, что n³ – n делится на 24 при любом нечетном n.
Задача 21:а) Докажите, что p² – 1 делится на 24, если p – простое число и p > 3.
б) Докажите, что p² – q² делится на 24, если p и q – простые числа, большие 3.
Задача 22:
Натуральные числа x, y, z таковы, что x² + y² = z². Докажите, что хотя бы одно из этих чисел делится на 3.
Задача 23:
a и b – натуральные числа, причем число a² + b² делится на 21. Докажите, что оно делится и на 441.
Задача 24:a, b, c – натуральные числа, причем a + b + c делится на 6. Докажите, что a³ + b³ + c³ тоже делится на 6.
Задача 25:
Три простых числа p, q и r, большие 3, образуют арифметическую прогрессию: p = p, q = p + d, r = p + 2d. Докажите, что d делится на 6.
Задача 26:
Докажите, что сумма квадратов трех натуральных чисел, уменьшенная на 7, не делится на 8.
Задача 27:
Сумма трех натуральных чисел, являющихся точными квадратами, делится на 9. Докажите, что из них можно выбрать два, разность которых также делится на 9.
Задача 28:
Найдите последнюю цифру числа 19891989.
Задача 29:
Найдите последнюю цифру числа 250.
Задача 30:
На какую цифру оканчивается число 777777?
Задача 31:Найдите остаток от деления 2¹ºº на 3.
Задача 32:Найдите остаток от деления 31989 на 7.
Задача 33:
Докажите, что 22225555 + 5555²²²² делится на 7.
Задача 34: Найдите последнюю цифру числа 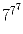 .
.
Задача 35:
а) p, p + 10, p + 14 – простые числа. Найдите p.
б) p, 2p + 1, 4p + 1 – простые числа. Найдите p.
Задача 36:
p и 8p² + 1 – простые числа. Найдите p.
Задача 37:
p и p² + 2 – простые числа. Докажите, что p³ + 2 – также простое число.
Задача 38:
Докажите, что не существует натуральных чисел a и b таких, что a² – 3b² = 8.
Задача 39:
а) Может ли сумма квадратов двух нечетных чисел быть квадратом целого числа?
б) Может ли сумма квадратов трех нечетных чисел быть квадратом целого числа?
Задача 40:
Докажите, что сумма квадратов пяти последовательных натуральных чисел не является точным квадратом.
Задача 41:
p, 4p² + 1 и 6p² + 1 – простые числа. Найдите p.
Ответ: p = 5. Рассмотрите остатки при делении на 5.
Задача 42:Докажите, что число 100 … 00500 … 001 (в каждой из двух групп по 100 нулей) не является кубом целого числа.
Задача 43:
Докажите, что a³ + b³ + 4 не является кубом целого числа ни при каких натуральных a и b.
Задача 44:
Докажите, что число 6n³ + 3 не является шестой степенью целого числа ни при каком натуральном n.
Задача 45:
x, y, z – натуральные числа, причем x² + y² = z². Докажите, что xy делится на 12.
| Задачная база >> Разное >> Математический кружок. 1-й год >> Делимость и остатки >> Остатки | Показать решения |