 |
 |
|
| Задачная база >> Разное >> Математический кружок. 1-й год >> Задачник первого года >> Конструкции и взвешивания | Показать решения |
|
|
| С.А.Генкин, И.В.Итенберг, Д.В.Фомин. Математический кружок. Задачник первого года. Конструкции и взвешивания |
|
|
Имеются двое песочных часов: на 7 минут и на 11 минут. Яйцо варится 15 минут. Как отмерить это время при помощи имеющихся часов?
Задача 19:
В кабине лифта 20-этажного дома есть две кнопки. При нажатии на одну из них лифт поднимается на 13 этажей, а при нажатии на другую – опускается на 8 этажей. Как попасть с 13-го этажа на 8-й?
Задача 20:
За один ход число, написанное на доске, разрешается либо заменить на удвоенное, либо стереть у него последнюю цифру. Вначале на доске написано число 458. Как за несколько ходов получить число 14?
Задача 21:
В ряд выложены карточки, на которых написаны числа 7, 8, 9, 4, 5, 6, 1, 2, 3. Разрешается взять несколько подряд лежащих карточек и переставить их в обратном порядке. Можно ли за три таких операции добиться расположения 1, 2, 3, 4, 5, 6, 7, 8, 9?
Задача 22:
В клетках таблицы 4 × 4 расставлены числа от 1 до 16 так, как показано на первом рисунке. Разрешается прибавить единицу одновременно ко всем числам любой строки или вычесть единицу из всех чисел любого столбца. Можно ли с помощью таких операций получить таблицу, приведенную на втором рисунке?
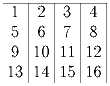

Задача 23:
Можно ли натуральные числа от 1 до 100 выписать в строчку так, чтобы разность любых двух соседних (из большего вычитают меньшее) была не меньше 50?
Задача 24:
Разложите гири с весами 1, 2, 3, …, 555 на три кучи, равные по весу.
Задача 25:
В клетках таблицы 4 × 4 расставьте числа, не равные нулю так, чтобы сумма чисел, стоящих в углах любого квадрата 2 × 2, 3 × 3 или 4 × 4, была равна нулю.
Задача 26:
Можно ли на ребрах куба расставить числа от 1 до 12 так, чтобы все суммы чисел на гранях были одинаковы?
Задача 27:
Можно ли расставить числа от 0 до 9 (каждое по разу) в кружках на рисунке так, чтобы все суммы в вершинах заштрихованных треугольников были одинаковы?
Задача 28:
Докажите, что в 400-значном числе 84198419 … 8419 можно вычеркнуть несколько цифр в начале и в конце так, чтобы сумма оставшихся цифр была равна 1984.
Задача 29:
Найдите двузначное число, сумма цифр которого не меняется при умножении на любое однозначное число.
Задача 30:
Существуют ли два последовательных натуральных числа, сумма цифр каждого из которых делится на 7?
Задача 31:
Существуют ли несколько положительных чисел, сумма которых равна 1, а сумма их квадратов меньше 0.01?
Задача 32:
Замок состоит из 64 одинаковых квадратных комнат, имеющих по двери в каждой стене и расположенных в виде квадрата 8 × 8. Полы в комнатах покрашены в белый цвет. Каждое утро маляр совершает прогулку по замку, причем, проходя через комнату, он перекрашивает пол в ней из белого цвета в черный, а из черного – в белый. Возможно ли, что когда-нибудь полы в замке окажутся покрашенными в шахматном порядке в черный и белый цвета?
Задача 33:
Как расположить на плоскости стола несколько пятаков, чтобы каждый из них касался ровно трех других?
Задача 34:
На складе в два штабеля сложены в произвольном порядке N контейнеров, которые имеют номера 1, 2, …, N. Автопогрузчик подъезжает к одному из штабелей, снимает сверху несколько контейнеров и устанавливает их на другой штабель. Докажите, что за 2N – 1 таких операций можно расположить все контейнеры в одном штабеле по порядку номеров.
Задача 35:
Есть 9 монет, одна из которых фальшивая (она легче настоящих). За два взвешивания определите фальшивую монету.
Задача 36:
Есть 10 мешков с монетами. Один из них целиком заполнен фальшивыми монетами, которые на один грамм легче настоящих. За одно взвешивание на весах со стрелкой, показывающей разность весов на чашках, определите «фальшивый» мешок.
Задача 37:
Имеется 101 монета. Среди них 100 одинаковых настоящих монет и одна фальшивая, отличающаяся от них по весу. Необходимо выяснить, легче или тяжелее фальшивая монета, чем настоящая. Как это сделать при помощи двух взвешиваний на чашечных весах без гирь?
Задача 38:
Есть 6 монет, из которых две – фальшивые, весящие меньше настоящих. За 3 взвешивания определите обе фальшивые монеты.
Задача 39:
Есть 10 мешков, некоторые из которых целиком заполнены фальшивыми монетами, а все остальные – настоящими. Фальшивая монета на один грамм легче настоящей. Про один из мешков точно известно, что он наполнен настоящими монетами. За одно взвешивание на весах со стрелкой определите все «фальшивые» мешки.
Задача 40:
Есть 5 монет, из которых три настоящих, одна – фальшивая, которая весит больше настоящей, и одна – фальшивая, которая весит меньше настоящей. За три взвешивания определите обе фальшивые монеты.
Задача 41:
Имеется 68 монет, различных по весу. За 100 взвешиваний найдите самую тяжелую и самую легкую монеты.
Задача 42:
Есть 64 камня с различными весами. За 68 взвешиваний найдите два самых тяжелых камня.
Задача 43:
Имеется 6 гирь: по паре зеленых, красных и белых. В каждой паре одна гиря тяжелая, а другая – легкая, причем все тяжелые гири весят одинаково и все легкие гири весят одинаково. За 2 взвешивания определите все 3 тяжелые гири.
Задача 44:
Есть 6 монет, из которых две – фальшивые, тяжелее настоящих на 0,1 грамма. Есть весы, которые реагируют только на разность весов на чашках, не меньшую 0,2 грамма. Как найти обе фальшивые монеты за 4 взвешивания?
Задача 45:
а) Есть 16 монет, одна из которых – фальшивая, однако неизвестно, в какую сторону она отличается от настоящей по весу. За 4 взвешивания определите фальшивую монету.
б) Есть 12 монет, одна из которых – фальшивая, однако неизвестно, в какую сторону она отличается от настоящей по весу. За 3 взвешивания найдите эту монету.
Задача 46:В качестве вещественного доказательства суду были предъявлены 14 монет. Суд знает, что из них 7 монет – настоящие, а остальные 7 монет – фальшивые, весящие меньше настоящих. Адвокат обвиняемого знает, какие именно монеты настоящие, а какие – фальшивые, и хочет убедить в этом суд. Как ему это сделать всего за 3 взвешивания?
| Задачная база >> Разное >> Математический кружок. 1-й год >> Задачник первого года >> Конструкции и взвешивания | Показать решения |