 |
 |
|
| Задачная база >> Разное >> Математический кружок. 2-й год >> Геометрия >> Два неравенства | Показать решения |
|
|
| С.А.Генкин, И.В.Итенберг, Д.В.Фомин. Математический кружок, 2-й год. Геометрия. Два неравенства |
|
|
Докажите, что при b + c > a, a + c > b, a + b > c, где a, b и c – положительные числа, существует треугольник со сторонами a, b и c.
Задача 2:
Докажите, что медиана AM в треугольнике ABC по длине больше, чем (AB + AC – BC)/2.
Задача 3:
Докажите, что из отрезков длины a, b и c можно составить треугольник тогда и только тогда, когда есть такие положительные x, y, z, что a = x + y, b = y + z, c = x + z.
Задача 4:
Докажите, что если AB = AC, то углы ABC и ACB равны.
Задача 5:
В треугольнике ABC длина медианы AM больше половины длины BC. Докажите, что угол BAC – острый.
Задача 6:
Докажите, что если из отрезков длины a, b и c можно
составить треугольник,то его можно составить и из отрезков длины
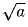 ,
, 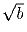 ,
, 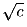 .
.
Задача 7:
ABCD – выпуклый 4-угольник, причем AB + BD < AC + CD. Докажите, что AB < AC.
Задача 8:
Центры трех непересекающихся кругов расположены на одной прямой. Докажите, что если окружность касается всех кругов, то ее радиус больше радиуса одного из них.
Задача 9:
Пусть ABCD и A1B1C1D1 – два выпуклых 4-угольника с соответственно равными сторонами. Докажите, что если ∠ A > ∠ A1, то ∠ B < ∠ B1, ∠ C > ∠ C1, ∠ D < ∠ D1.
Задача 10:
Докажите, что медиана треугольника, заключенная между двумя его неравными сторонами, образует больший угол с меньшей из двух этих сторон.
Задача 11:
Могут ли в прямолинейной пятиконечной звезде ABCDEFGHIK выполняться неравенства: AB > BC, CD > DE, EF > FG, GH > HI, IK > KA?
Задача 12:Дан равнобедренный треугольник ABC с углом при вершине B, равным 20 градусов. Докажите, что а) AB < 3AC; б) AB > 2AC.
Задача 13:
Периметр пятиконечной звезды с вершинами в вершинах выпуклого пятиугольника Ф, периметр самого Ф, и периметр внутреннего пятиугольника звезды – простые числа. Докажите, что их сумма не меньше 20.
Задача 14:
На каждой стороне квадрата отмечено по точке. Докажите, что периметр образованного ими четырехугольника не меньше удвоенной длины диагонали квадрата.
| Задачная база >> Разное >> Математический кружок. 2-й год >> Геометрия >> Два неравенства | Показать решения |