 |
 |
|
| Задачная база >> Разное >> Математический кружок. 2-й год >> Комбинаторика-2 >> Треугольник Паскаля | Показать решения |
|
|
| С.А.Генкин, И.В.Итенберг, Д.В.Фомин. Математический кружок, 2-й год. Комбинаторика-2. Треугольник Паскаля |
|
|
Человек имеет 10 друзей и в течение нескольких дней приглашает некоторых из них в гости так, что компания ни разу не повторяется (в какой-то из дней он может не приглашать никого). Сколько дней он может так делать?
Задача 23:
Лестница состоит из 7 ступенек, не считая верхней и нижней площадок. Спускаясь, можно перепрыгивать через некоторые ступеньки (можно даже через все 7). Сколькими способами можно спуститься по этой лестнице?
Задача 24:
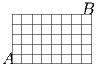
План города имеет схему, изображенную на рисунке. На всех улицах введено одностороннее движение: можно ехать только «вправо» или «вверх». Сколько есть разных маршрутов, ведущих из точки A в точку B?
Докажите, что из n предметов четное число предметов можно выбрать 2n – 1 способами.
Задача 26:
Докажите, что
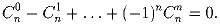
Задача 27:
Докажите, что каждое число a в треугольнике Паскаля равно сумме чисел предыдущей правой диагонали, начиная с самого левого вплоть до стоящего справа над числом a.
Задача 28:
Докажите, что каждое число a в треугольнике Паскаля равно сумме чисел в предыдущей левой диагонали, начиная с самого правого вплоть до стоящего слева над числом a.
Задача 29:
Докажите, что каждое число a в треугольнике Паскаля, уменьшенное на 1, равно сумме всех чисел, заполняющих параллелограмм, ограниченный теми правой и левой диагоналями, на пересечении которых стоит число a (сами эти диагонали в рассматриваемый параллелограмм не включаются).
Задача 30:
Докажите, что
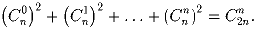
| Задачная база >> Разное >> Математический кружок. 2-й год >> Комбинаторика-2 >> Треугольник Паскаля | Показать решения |