 |
 |
|
| Задачная база >> Разное >> Математический кружок. 2-й год >> Комбинаторика-2 >> Треугольник Паскаля | Убрать решения |
|
|
| С.А.Генкин, И.В.Итенберг, Д.В.Фомин. Математический кружок, 2-й год. Комбинаторика-2. Треугольник Паскаля |
|
|
Человек имеет 10 друзей и в течение нескольких дней приглашает некоторых из них в гости так, что компания ни разу не повторяется (в какой-то из дней он может не приглашать никого). Сколько дней он может так делать?
Решение:
2¹º = 1024.
Задача 23:Лестница состоит из 7 ступенек, не считая верхней и нижней площадок. Спускаясь, можно перепрыгивать через некоторые ступеньки (можно даже через все 7). Сколькими способами можно спуститься по этой лестнице?
Решение:
27 = 128.
Задача 24:
План города имеет схему, изображенную на рисунке. На всех улицах введено одностороннее движение: можно ехать только «вправо» или «вверх». Сколько есть разных маршрутов, ведущих из точки A в точку B?
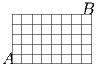
Для удобства назовем улицей отрезок изображенной
сетки, соединяющий два соседних узла. Ясно, что каждый
маршрут содержит ровно 13 улиц, причем 8 из них расположены по
горизонтали, а 5 – по вертикали. Сопоставим каждому маршруту
последовательность букв Г и В следующим образом: при прохождении
«горизонтальной» улицы маршрута будем дописывать в
последовательность букву Г, а при прохождении «вертикальной»
улицы – букву В.
Каждая последовательность
содержит 13 букв – 8 букв Г и 5 букв В. Осталось вычислить
количество таких последовательностей. Последовательность
однозначно задается набором из 5 мест, на которых в ней стоят
буквы В (или набором из 8 мест, на которых стоят буквы Г).
Пять мест из 13 можно выбрать 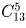 способами. Поэтому число
возможных последовательностей, а значит, и число возможных
маршрутов, равно
способами. Поэтому число
возможных последовательностей, а значит, и число возможных
маршрутов, равно 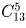 .
.
Задача 25:
Докажите, что из n предметов четное число предметов можно выбрать 2n – 1 способами.
Решение:
Сумма чисел, стоящих на четных местах в n-й строке треугольника Паскаля, равна сумме чисел, стоящих на нечетных местах той же строки.
Задача 26:Докажите, что
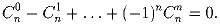
Решение:
Сумма чисел, стоящих на четных местах в n-й строке треугольника Паскаля, равна сумме чисел, стоящих на нечетных местах той же строки.
Задача 27:
Докажите, что каждое число a в треугольнике Паскаля равно сумме чисел предыдущей правой диагонали, начиная с самого левого вплоть до стоящего справа над числом a.
Решение:
Индукция по количеству чисел на диагонали.
Задача 28:Докажите, что каждое число a в треугольнике Паскаля равно сумме чисел в предыдущей левой диагонали, начиная с самого правого вплоть до стоящего слева над числом a.
Решение:
Индукция по количеству чисел на диагонали.
Задача 29:Докажите, что каждое число a в треугольнике Паскаля, уменьшенное на 1, равно сумме всех чисел, заполняющих параллелограмм, ограниченный теми правой и левой диагоналями, на пересечении которых стоит число a (сами эти диагонали в рассматриваемый параллелограмм не включаются).
Задача 30:
Докажите, что
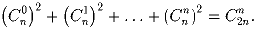
Решение:
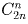 – количество путей, ведущих из вершины
треугольника Паскаля к числу, стоящему на n-м месте в 2n-й
строке. Каждый такой путь проходит ровно через одно число n-й
строки. При этом количество путей, проходящих через число,
стоящее на k-ом месте, равно
– количество путей, ведущих из вершины
треугольника Паскаля к числу, стоящему на n-м месте в 2n-й
строке. Каждый такой путь проходит ровно через одно число n-й
строки. При этом количество путей, проходящих через число,
стоящее на k-ом месте, равно 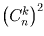 .
.
| Задачная база >> Разное >> Математический кружок. 2-й год >> Комбинаторика-2 >> Треугольник Паскаля | Убрать решения |