 |
 |
|
| Задачная база >> Разное >> Математический кружок. 2-й год >> Неравенства >> Неравенства на все вкусы | Показать решения |
|
|
| С.А.Генкин, И.В.Итенберг, Д.В.Фомин. Математический кружок, 2-й год. Неравенства. Неравенства на все вкусы |
|
|
Вокруг экватора натянули веревку. Затем ее удлинили на 1 см и опять натянули, приподняв в одном месте. Сможет ли человек пройти в образовавшийся зазор?
Задача 67:
Представьте себе, что Землю «раскатали в колбаску» так, чтобы она достала до Солнца. Какой толщины будет эта «колбаска»? Постарайтесь ошибиться не более, чем в 10 раз.
Задача 68:
Поместится ли все население Земли, все здания и сооружния на ней в куб с длиной ребра 3 километра?
Задача 69:
Представьте себе, что вы стоите на Дворцовой набережной Невы. Как вам, используя только подручные средства и глазомер, оценить высоту шпиля на соборе Петропавловской крепости?
Задача 70:
Докажите, что 100! < 50¹ºº.
Задача 71:
n – натуральное число. Докажите, что
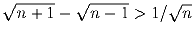 .
.
Задача 72:
1 > x > y > 0. Докажите, что (x – y)/(1 – xy) < 1.
Задача 73:
a, b, c, d ≥ 0, причем c + d ≤ a, c + d ≤ b. Докажите, что ad + bc ≤ ab.
Задача 74:
Существует ли набор чисел, сумма которых равна 1, а сумма их квадратов меньше 0.01?
Задача 75:
a, b, c > 0 и abc = 1. Известно, что a + b + c > 1/a + 1/b + + 1/c. Докажите, что ровно одно из чисел a, b, c больше 1.
Задача 76:
x, y – числа из отрезка [0;1]. Докажите неравенство
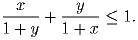
Задача 77:
a, b, c – натуральные числа и 1/a + 1/b + 1/c < 1. Докажите, что 1/a + 1/b + 1/c ≤ 41/42.
Задача 78:
x, y, z – положительные числа. Докажите неравенство
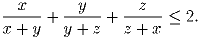
Задача 79:
Докажите, что
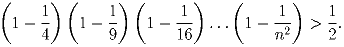
Задача 80:
Докажите, что для любого x выполнено неравенство x4 – x³ + 3x² – 2x + 2 ≥ 0.
Задача 81:
Числа a, b, c, d – из отрезка [0;1]. Докажите, что (a + b + c + d + 1)² ≥ 4(a² + b² + c² + d²).
Задача 82:
x, y > 0. Через S обозначим наименьшее из чисел x, 1/y, y + 1/x. Какое максимальное значение может принимать величина S?
Задача 83:
a, b, c, d – положительные числа. Докажите, что по крайней мере одно из неравенств
1) a + b < c + d;
2) (a + b)cd < ab(c + d);
3) (a + b)(c + d) < ab + cd
неверно.
Задача 84:
Докажите, что три неравенства
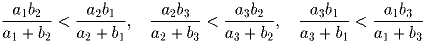
Задача 85:
Докажите, что если x + y + z ≥ xyz, то x² + y² + z² ≥ xyz.
| Задачная база >> Разное >> Математический кружок. 2-й год >> Неравенства >> Неравенства на все вкусы | Показать решения |