Задача 1:
Сформулируйте признаки делимости на 2, 3, 4, 5, 9, 10, 25,
50, 100.
Задача 2:
Почему верны признаки «Число делится на 2 тогда и только
тогда, когда его последняя цифра делится на 2» и «Число делится
на 5 тогда и только тогда, когда его последняя цифра делится на
5» и не верны аналогичные признаки для других однозначных чисел?
Задача 3:
Почему верен признак «Число делится на 4 тогда и только
тогда, когда число, образованное двумя его последним цифрами
делится на 4»? Сформулируйте аналогичные признаки делимости для
чисел 25 и 50. Что общего у этих чисел с числом 4?
Задача 4:
Назовем число «забавным», если все его цифры делятся на 4.
А делится ли «забавное» число на 4? Существуют ли не
«забавные» числа, которые делятся на 4?
Задача 5:
Сформулируйте и докажите признаки делимости на 8 и 125. (А на 2
n
и 5
n?)
Задача 6:
Сформулируйте признаки делимости на 3 и на 9. Верны ли
аналогичные признаки для других однозначных чисел? Почему всякое
число вида 10 … 0 при делении на 9 (и на 3) дает в остатке 1?
Задача 7:
Какой остаток от деления на 3 и на 9 дает число вида
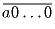
? Докажите, что число и его сумма цифр дают
при делении на 9 одинаковые остатки. Докажите, что то же верно
при делении на 3.
Задача 8:
Задумайте число. Прибавьте 2, умножьте на 3, возведите в квадрат,
прибавьте 36, посчитайте сумму цифр, еще раз, и еще,
пока не получите однозначное число. Отнимите от него 4.
Найдите n-ую букву алфавита, придумайте
на нее название страны, на третью букву названия придумайте животное.
Так вот, в Дании носороги не водятся!
Объясните этот фокус.
Задача 9:
Докажите, что 11 … 1 (27 единиц) делится на 27. Верен ли
признак делимости на 27, аналогичный признакам делимости на 3 и
9?
Задача 10:
Как проверить, делится ли число на а) 6; б) 12; в) 15;
г) 18; д) 30; е) 45; ж) 75; з) 225?
Задача 11:
При каких a число
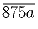
делится на 6?
Задача 12:
Из двузначного числа вычли число, получающееся из него же
перестановкой цифр. Докажите, что результат делится на 9.
Задача 13:
Шестиклассник Петя перемножил все числа от 1 до 2000. У
полученного числа он подсчитал сумму цифр, затем подсчитал сумму
цифр результата, и так далее, пока не получил число, состоящее из
одной цифры. Какое?
Задача 14:
Натуральное число возвели в квадрат. Может ли результат
оканчиваться на 66?
Задача 15:
Ольга Сергеевна называет три цифры. А Константин
Александрович говорит, что всегда сможет составить из них одно-,
двух- или трёхзначное число, делящееся на 3. Прав ли он?
Задача 16:
В ряд стоят 100 фишек. Разрешается поменять местами любые
две фишки, стоящие через одну. Можно ли переставить все фишки в
обратном порядке?
Задача 17:
В трёхзначном числе n первые две цифры одинаковые, а
последняя цифра – 5. Кроме того, известно, что n дает остаток 8
при делении на некоторое однозначное число. Найдите n.
Задача 18:
На доске написано число 1. Каждую секунду к числу на доске
прибавляют сумму его цифр. Может ли через некоторое время на
доске появиться число 123456?
Задача 19:
Из числа 123123123123 вычеркните несколько цифр так, чтобы
получилось наибольшее возможное число, кратное 9.
Задача 20:
Может ли число, записываемое при помощи 100 нулей, 100 единиц
и 100 двоек, быть точным квадратом?
Задача 21:
Из трёхзначного числа вычли сумму его цифр. С полученным
числом проделали то же самое и так далее, 120 раз. Докажите, что
в результате получился нуль.
Задача 22:
Шесть игральных кубиков нанизали на спицу (протыкая ею центры
противоположных граней кубиков) так, что каждый может вращаться
независимо от остальных. На гранях каждого кубика написаны все
цифры от 1 до 6, причём сумма цифр на противоположных гранях
равна 7. Спицу положили на стол и прочитали число, образованное
цифрами на верхних гранях кубиков. Докажите, что можно так
повернуть кубики, чтобы это число делилось на 7.
Задача 23:
В десятизначном числе все цифры встречаются по разу. Может ли
оно делиться на 11?


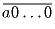 ? Докажите, что число и его сумма цифр дают
при делении на 9 одинаковые остатки. Докажите, что то же верно
при делении на 3.
Задача 8:
Задумайте число. Прибавьте 2, умножьте на 3, возведите в квадрат,
прибавьте 36, посчитайте сумму цифр, еще раз, и еще,
пока не получите однозначное число. Отнимите от него 4.
Найдите n-ую букву алфавита, придумайте
на нее название страны, на третью букву названия придумайте животное.
Так вот, в Дании носороги не водятся!
? Докажите, что число и его сумма цифр дают
при делении на 9 одинаковые остатки. Докажите, что то же верно
при делении на 3.
Задача 8:
Задумайте число. Прибавьте 2, умножьте на 3, возведите в квадрат,
прибавьте 36, посчитайте сумму цифр, еще раз, и еще,
пока не получите однозначное число. Отнимите от него 4.
Найдите n-ую букву алфавита, придумайте
на нее название страны, на третью букву названия придумайте животное.
Так вот, в Дании носороги не водятся!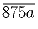 делится на 6?
Задача 12:
Из двузначного числа вычли число, получающееся из него же
перестановкой цифр. Докажите, что результат делится на 9.
Задача 13:
Шестиклассник Петя перемножил все числа от 1 до 2000. У
полученного числа он подсчитал сумму цифр, затем подсчитал сумму
цифр результата, и так далее, пока не получил число, состоящее из
одной цифры. Какое?
Задача 14:
Натуральное число возвели в квадрат. Может ли результат
оканчиваться на 66?
Задача 15:
Ольга Сергеевна называет три цифры. А Константин
Александрович говорит, что всегда сможет составить из них одно-,
двух- или трёхзначное число, делящееся на 3. Прав ли он?
Задача 16:
В ряд стоят 100 фишек. Разрешается поменять местами любые
две фишки, стоящие через одну. Можно ли переставить все фишки в
обратном порядке?
Задача 17:
В трёхзначном числе n первые две цифры одинаковые, а
последняя цифра – 5. Кроме того, известно, что n дает остаток 8
при делении на некоторое однозначное число. Найдите n.
Задача 18:
На доске написано число 1. Каждую секунду к числу на доске
прибавляют сумму его цифр. Может ли через некоторое время на
доске появиться число 123456?
Задача 19:
Из числа 123123123123 вычеркните несколько цифр так, чтобы
получилось наибольшее возможное число, кратное 9.
Задача 20:
Может ли число, записываемое при помощи 100 нулей, 100 единиц
и 100 двоек, быть точным квадратом?
Задача 21:
Из трёхзначного числа вычли сумму его цифр. С полученным
числом проделали то же самое и так далее, 120 раз. Докажите, что
в результате получился нуль.
Задача 22:
Шесть игральных кубиков нанизали на спицу (протыкая ею центры
противоположных граней кубиков) так, что каждый может вращаться
независимо от остальных. На гранях каждого кубика написаны все
цифры от 1 до 6, причём сумма цифр на противоположных гранях
равна 7. Спицу положили на стол и прочитали число, образованное
цифрами на верхних гранях кубиков. Докажите, что можно так
повернуть кубики, чтобы это число делилось на 7.
Задача 23:
В десятизначном числе все цифры встречаются по разу. Может ли
оно делиться на 11?
делится на 6?
Задача 12:
Из двузначного числа вычли число, получающееся из него же
перестановкой цифр. Докажите, что результат делится на 9.
Задача 13:
Шестиклассник Петя перемножил все числа от 1 до 2000. У
полученного числа он подсчитал сумму цифр, затем подсчитал сумму
цифр результата, и так далее, пока не получил число, состоящее из
одной цифры. Какое?
Задача 14:
Натуральное число возвели в квадрат. Может ли результат
оканчиваться на 66?
Задача 15:
Ольга Сергеевна называет три цифры. А Константин
Александрович говорит, что всегда сможет составить из них одно-,
двух- или трёхзначное число, делящееся на 3. Прав ли он?
Задача 16:
В ряд стоят 100 фишек. Разрешается поменять местами любые
две фишки, стоящие через одну. Можно ли переставить все фишки в
обратном порядке?
Задача 17:
В трёхзначном числе n первые две цифры одинаковые, а
последняя цифра – 5. Кроме того, известно, что n дает остаток 8
при делении на некоторое однозначное число. Найдите n.
Задача 18:
На доске написано число 1. Каждую секунду к числу на доске
прибавляют сумму его цифр. Может ли через некоторое время на
доске появиться число 123456?
Задача 19:
Из числа 123123123123 вычеркните несколько цифр так, чтобы
получилось наибольшее возможное число, кратное 9.
Задача 20:
Может ли число, записываемое при помощи 100 нулей, 100 единиц
и 100 двоек, быть точным квадратом?
Задача 21:
Из трёхзначного числа вычли сумму его цифр. С полученным
числом проделали то же самое и так далее, 120 раз. Докажите, что
в результате получился нуль.
Задача 22:
Шесть игральных кубиков нанизали на спицу (протыкая ею центры
противоположных граней кубиков) так, что каждый может вращаться
независимо от остальных. На гранях каждого кубика написаны все
цифры от 1 до 6, причём сумма цифр на противоположных гранях
равна 7. Спицу положили на стол и прочитали число, образованное
цифрами на верхних гранях кубиков. Докажите, что можно так
повернуть кубики, чтобы это число делилось на 7.
Задача 23:
В десятизначном числе все цифры встречаются по разу. Может ли
оно делиться на 11?