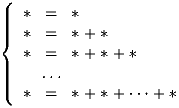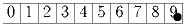Задача 1:
Игра начинается с числа 60. За ход
разрешается уменьшить имеющееся число на любой из его делителей.
Проигрывает тот, кто получит ноль.
Задача 2:
Волк и Заяц играют в следующую игру: на доске написано
некоторое натуральное число с ненулевой последней цифрой.
Ход состоит в том, что из числа вычитают какую-нибудь его
ненулевую цифру и пишут результат вместо старого числа.
Выигрывает тот, кто первым получит нуль.
Задача 3:
Имеется две кучи конфет: в первой – 40, во второй – 45. За
ход нужно одну кучу съесть, а другую разделить на две (не
обязательно равные). Проигрывает тот, кто не может сделать ход.
Задача 4:
Имеется две кучи конфет: в первой – 100, во второй – 201. За
ход разрешается съесть из одной кучки любое число конфет,
являющееся делителем количества конфет в другой кучке.
Выигрывает тот, кто съедает последнюю конфету.
Задача 5:
Два игрока ставят по очереди числа вместо звездочек
в следующей системе равенств:
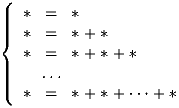
(в последнем равенстве справа 8 слагаемых). Второй игрок выигрывает,
если все равенства выполняются, в противном случае выигрывает первый.
Задача 6:
Имеется полоска клетчатой бумаги длиной 10
клеток. В крайней правой ее клетке стоит шашка (рис. 1). Двое
играющих по очереди передвигают ее влево на одну или две клетки.
Проигрывает тот, кому некуда ходить.
6cm
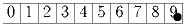
Рис 1.
Задача 7:
Кто выигрывает в игре Баше, если длина полоски составляет 11
клеток? 12 клеток? 13 клеток? 2000 клеток?
Задача 8:
Изменим правила игры Баше: теперь за один ход
можно сдвигать шашку на 1, 2, 3, 4 или 5 клеток, а длина
полоски – 13 клеток.
Задача 9:
А теперь в игре Баше можно сдвигать шашку
на 3, 6, 9 или 12 клеток, а длина полоски – 40 клеток.
Задача 10:
Проанализируйте игру Баше, где можно сдвигать шашку на 1, 3 или 4
клетки, а длина полоски – 15 клеток. А что можно сказать про
случай, если длина полоски – 2000 клеток?