Задача 1:
Можно ли выложить шахматную доску тридцатью двумя доминошками так,
чтобы 17 из них были расположены горизонтально, а 15 – вертикально?
Задача 2:
Можно ли выложить квадрат 8 × 8, используя 15
прямоугольников 1 × 4 и один уголок вида
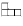
?
Задача 3:
Можно ли выложить прямоугольник 6 × 10 прямоугольниками
1 × 4?
Задача 4:
Можно ли сложить квадрат 6 × 6 с помощью 11 прямоугольников
1 × 3 и одного уголка вида

?
Задача 5:
На каждой клетке доски 5 × 5 сидит жук. В некоторый момент
времени все жуки взлетают и приземляются на соседние по стороне клетки.
Докажите, что при этом окажется хотя бы одна пустая клетка.
Задача 6:
Из доски 8 × 8 вырезали угловую клетку. Можно ли
оставшуюся часть разрезать на прямоугольники 3 × 1?
Задача 7:
Фигура «верблюд» ходит по шахматной доске ходом типа (1, 3).
Можно ли пройти ходом «верблюда» с произвольного поля на соседнее?
Задача 8:
Можно ли доску размером 10 × 10 покрыть фигурами вида
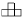
?
Задача 9:
Дана доска 12 × 12.
В левом нижнем углу стоят 9 шашек, образуя квадрат 3 × 3.
За один ход можно выбрать какие-то две шашки и переставить одну
из них симметрично относительно другой (не выходя при этом за
пределы доски). Можно ли за несколько ходов переместить эти шашки
так, чтоб они образовали квадрат 3 × 3 в правом нижнем углу?
Задача 10:
В каждой клетке квадрата 9 × 9 сидит жук. По команде
каждый жук перелетает на одну из соседних по диагонали клеток.
Доказать, что по крайней мере 9 клеток после этого окажутся
свободными.
Задача 11:
Замок имеет форму правильного треугольника, разделенного на 25
маленьких залов той же формы. В каждой стене между залами проделана
дверь. Путник ходит по замку, не посещая более одного раза ни один из
залов. Найти наибольшее число залов, которое ему удастся посетить.
Задача 12:
Дан куб 6 × 6 × 6. Докажите, что его нельзя
разбить на параллелепипеды 4 × 1 × 1.
Задача 13:
Докажите, что числа от 40 до 99 нельзя разбить на группы по 4
числа так, чтобы числа каждой группы в одном разряде совпадали,
а цифры другого разряда шли бы подряд (например «54, 55, 56, 57»;
«44, 54, 64, 74»)
Указание: Попытайтесь закодировать эту задачу так, чтобы оправдать её
наличие в теме «раскраски».
Задача 14:
Докажите, что трёхзначные числа нельзя разбить на группы по 4 так,
чтобы числа в каждой группе совпадали во всех разрядах кроме одного,
а в оставшемся разряде цифры шли бы подряд.


 ?
Задача 3:
Можно ли выложить прямоугольник 6 × 10 прямоугольниками
1 × 4?
Задача 4:
Можно ли сложить квадрат 6 × 6 с помощью 11 прямоугольников
1 × 3 и одного уголка вида
?
Задача 3:
Можно ли выложить прямоугольник 6 × 10 прямоугольниками
1 × 4?
Задача 4:
Можно ли сложить квадрат 6 × 6 с помощью 11 прямоугольников
1 × 3 и одного уголка вида  ?
Задача 5:
На каждой клетке доски 5 × 5 сидит жук. В некоторый момент
времени все жуки взлетают и приземляются на соседние по стороне клетки.
Докажите, что при этом окажется хотя бы одна пустая клетка.
Задача 6:
Из доски 8 × 8 вырезали угловую клетку. Можно ли
оставшуюся часть разрезать на прямоугольники 3 × 1?
Задача 7:
Фигура «верблюд» ходит по шахматной доске ходом типа (1, 3).
Можно ли пройти ходом «верблюда» с произвольного поля на соседнее?
Задача 8:
Можно ли доску размером 10 × 10 покрыть фигурами вида
?
Задача 5:
На каждой клетке доски 5 × 5 сидит жук. В некоторый момент
времени все жуки взлетают и приземляются на соседние по стороне клетки.
Докажите, что при этом окажется хотя бы одна пустая клетка.
Задача 6:
Из доски 8 × 8 вырезали угловую клетку. Можно ли
оставшуюся часть разрезать на прямоугольники 3 × 1?
Задача 7:
Фигура «верблюд» ходит по шахматной доске ходом типа (1, 3).
Можно ли пройти ходом «верблюда» с произвольного поля на соседнее?
Задача 8:
Можно ли доску размером 10 × 10 покрыть фигурами вида 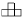 ?
Задача 9:
Дана доска 12 × 12.
В левом нижнем углу стоят 9 шашек, образуя квадрат 3 × 3.
За один ход можно выбрать какие-то две шашки и переставить одну
из них симметрично относительно другой (не выходя при этом за
пределы доски). Можно ли за несколько ходов переместить эти шашки
так, чтоб они образовали квадрат 3 × 3 в правом нижнем углу?
Задача 10:
В каждой клетке квадрата 9 × 9 сидит жук. По команде
каждый жук перелетает на одну из соседних по диагонали клеток.
Доказать, что по крайней мере 9 клеток после этого окажутся
свободными.
Задача 11:
Замок имеет форму правильного треугольника, разделенного на 25
маленьких залов той же формы. В каждой стене между залами проделана
дверь. Путник ходит по замку, не посещая более одного раза ни один из
залов. Найти наибольшее число залов, которое ему удастся посетить.
Задача 12:
Дан куб 6 × 6 × 6. Докажите, что его нельзя
разбить на параллелепипеды 4 × 1 × 1.
Задача 13:
Докажите, что числа от 40 до 99 нельзя разбить на группы по 4
числа так, чтобы числа каждой группы в одном разряде совпадали,
а цифры другого разряда шли бы подряд (например «54, 55, 56, 57»;
«44, 54, 64, 74»)
?
Задача 9:
Дана доска 12 × 12.
В левом нижнем углу стоят 9 шашек, образуя квадрат 3 × 3.
За один ход можно выбрать какие-то две шашки и переставить одну
из них симметрично относительно другой (не выходя при этом за
пределы доски). Можно ли за несколько ходов переместить эти шашки
так, чтоб они образовали квадрат 3 × 3 в правом нижнем углу?
Задача 10:
В каждой клетке квадрата 9 × 9 сидит жук. По команде
каждый жук перелетает на одну из соседних по диагонали клеток.
Доказать, что по крайней мере 9 клеток после этого окажутся
свободными.
Задача 11:
Замок имеет форму правильного треугольника, разделенного на 25
маленьких залов той же формы. В каждой стене между залами проделана
дверь. Путник ходит по замку, не посещая более одного раза ни один из
залов. Найти наибольшее число залов, которое ему удастся посетить.
Задача 12:
Дан куб 6 × 6 × 6. Докажите, что его нельзя
разбить на параллелепипеды 4 × 1 × 1.
Задача 13:
Докажите, что числа от 40 до 99 нельзя разбить на группы по 4
числа так, чтобы числа каждой группы в одном разряде совпадали,
а цифры другого разряда шли бы подряд (например «54, 55, 56, 57»;
«44, 54, 64, 74»)