Задача 1:
Какое наибольшее число слонов можно добавить к шести ладьям так,
чтобы ни одна из шахматных фигур на доске не била другую?
Задача 2:
В классе 21 человек. Никакие две девочки не дружат с одинаковым
количеством мальчиков. Какое наибольшее количество девочек может быть
в классе?
Задача 3:
Может ли шахматный конь (который ходит по правилам) обойти все
поля доски 4 × 4, побывав на каждом поле ровно один раз, и
вернуться на ту же клетку? Начинать разрешается на любом поле.
Задача 4:
Разрежьте правильный шестиугольник на 8 равных частей.
Задача 5:
Три девочки и три мальчика в течение года решали одни и те же
задачи. Катя решила ¾ всех задач и еще ¼ от того, что
решил Петя. Лена решила ½ всех задач и еще
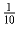
того,
что решил Вася. Маша решила
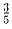
всех задач и еще
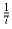
от
того, что решил Федя. Какая из девочек решила больше всех задач?
Задача 6:
Три команды играли в КВН. Перед игрой игрок Иванов перешел из
первой команды во вторую, игрок Сидоров перешел из второй команды в
третью, а игрок Петров перешел из третьей команды в первую. После
этого средний возраст первой команды увеличился на 1 неделю, второй –
увеличился на 2 недели, а третьей – уменьшился на 4 недели. Известно,
что в первой и во второй команде по 12 игроков. Сколько игроков в
третьей команде?
Задача 7:
В квадрате 3 × 3 расставлены числа так, чтобы суммы чисел в
каждой строке, каждом столбце и на каждой большой диагонали равны
нулю. Известно, что сумма квадратов чисел в верхней строке равна 2000.
Чему может быть равна сумма квадратов чисел в нижней строке?


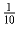 того,
что решил Вася. Маша решила
того,
что решил Вася. Маша решила 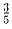 всех задач и еще
всех задач и еще 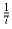 от
того, что решил Федя. Какая из девочек решила больше всех задач?
Задача 6:
Три команды играли в КВН. Перед игрой игрок Иванов перешел из
первой команды во вторую, игрок Сидоров перешел из второй команды в
третью, а игрок Петров перешел из третьей команды в первую. После
этого средний возраст первой команды увеличился на 1 неделю, второй –
увеличился на 2 недели, а третьей – уменьшился на 4 недели. Известно,
что в первой и во второй команде по 12 игроков. Сколько игроков в
третьей команде?
Задача 7:
В квадрате 3 × 3 расставлены числа так, чтобы суммы чисел в
каждой строке, каждом столбце и на каждой большой диагонали равны
нулю. Известно, что сумма квадратов чисел в верхней строке равна 2000.
Чему может быть равна сумма квадратов чисел в нижней строке?
от
того, что решил Федя. Какая из девочек решила больше всех задач?
Задача 6:
Три команды играли в КВН. Перед игрой игрок Иванов перешел из
первой команды во вторую, игрок Сидоров перешел из второй команды в
третью, а игрок Петров перешел из третьей команды в первую. После
этого средний возраст первой команды увеличился на 1 неделю, второй –
увеличился на 2 недели, а третьей – уменьшился на 4 недели. Известно,
что в первой и во второй команде по 12 игроков. Сколько игроков в
третьей команде?
Задача 7:
В квадрате 3 × 3 расставлены числа так, чтобы суммы чисел в
каждой строке, каждом столбце и на каждой большой диагонали равны
нулю. Известно, что сумма квадратов чисел в верхней строке равна 2000.
Чему может быть равна сумма квадратов чисел в нижней строке?