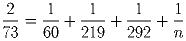Задача 1: Решите задачу из папируса Ринда: найти натуральное n такое, что

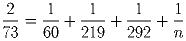
Задача 2: На пол разлили больше десяти литров сгущенки. Как собрать с пола ровно шесть литров с помощью только девятилитровой кастрюли и пятилитровой кружки?

Задача 3: Алла, Галя, Лена и Марина играли в настольный теннис «пара на пару». Марина младше Гали. Лена старше, чем любая из ее противниц. Марина старше своей партнерши. Алле и Гале вдвоем больше лет, чем Лене и Марине вместе. Кто с кем играл и как распределить девушек по возрасту? Обоснуйте ваш ответ.

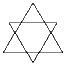
Задача 4: На рисунке изображены два правильных треугольника. Сторона большего из них равна 5 см, а меньшего – 4 см. Найдите периметр образовавшегося шестиугольника.

Задача 5: Костя и Рома играют в интересную игру на прямоугольнике а) 10 × 10; б) 10 × 11 с вырезанной внутренностью (оставлены только те клетки, которые примыкают к границе). За каждый ход разрешается вырезать любой прямоугольник, целиком состоящий из клеток, при условии, что оставшаяся часть не распадается на два куска. Проигрывает тот, кто не может сделать хода. Первым ходит Костя. Кто выиграет при правильной игре?

Задача 6: Назовем пятизначное число неразложимым, если его нельзя представить в виде произведения двух трёхзначных чисел. Какое наибольшее количество неразложимых чисел может идти подряд?