Задача 1:
Не находя суммы 52715223 + 71337651 + 53258554 + 633164334 + 71574116 + 4325988, выберите верный ответ:
а) 886375457; б) 886375478; в) 886375866; г) 86375942.
Задача 2:
Некоторые семиклассники взяли из комнаты N0 фломастеры для стенгазеты. Из
них несколько мальчиков взяли по целой пачке из 6 фломастеров, несколько
девочек забрали по 8 фломастеров разных цветов, а восьми опоздавшим
досталось по фломастеру синего цвета. В конце смены Борис Юрьевич хочет
собрать с семиклассников 155 фломастеров. Сочтут ли школьники это требование
выполнимым?
Задача 3:
Каждый следующий день смены семиклассник получает в два раза меньше
комариных укусов, чем в предыдущий. Может ли он за два дня подряд получить
2000 укусов?
Задача 4:
ЛМШонок Петя охотился на комаров. В первый день ему удалось убить только
двоих, но с каждым днем его квалификация повышалась и ему удавалось убивать
вдвое больше комаров, чем в предыдущий. Мог ли он в двадцать пятый день
убить 33554434 комара?
Задача 5:
Какие из утверждений верны:
а) если число при делении на 8 дает остаток 3, то при делении на 4 оно также
дает остаток 3;
б) если число при делении на 4 дает остаток 3, то при делении на 8 остаток
сохраняется;
в) если число при делении на 15 дает остаток 7, то при делении на 5 остаток
не равен 3;
г) если число при делении на 15 дает остаток 3, то при делении на 9 остаток
не равен 6?
Задача 6:
Генерал построил солдат в колонну по 4, но при этом солдат Иванов остался
лишним. Тогда генерал построил солдат в колонну по 5. И снова Иванов остался
лишним. Когда же и в колонне по 6 Иванов остался лишним, генерал посулил ему
наряд вне очереди, после чего в колонне по 7 Иванов нашел себе место и
никого лишнего не осталось. Какое наименьшее количество солдат могло быть у
генерала?
Задача 7:
Дождь над Вишкилем начался в полночь и лил ровно 10000 минут. Могло ли
случиться, что сразу после этого выглянуло солнце?
Задача 8:
На сколько нулей заканчивается число 2000!?
Задача 9:
Найдите последнюю цифру числа а) 2001²ºº¹;
б) 549
49; в) 345673
376543; г)
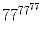
.
Задача 10:
Найдите две последние цифры числа а) 1999
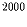
;
б) 16
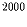
.
Задача 11:
Докажите, что Александр Юрьевич должен отпраздновать свое 28-летие в такой
же день недели, в какой он родился.
Задача 12:
В последовательности цифр каждая цифра, начиная с пятой, равна последней
цифре суммы четырех предыдущих. Последовательность начинается с цифр
1234096Может ли в ней встретиться комбинация цифр 1999?
Задача 13:
Найдите последнюю ненулевую цифру числа 2000!
Задача 14:
Пушкин родился 6 июня 1799 года (по новому стилю). Какой это день недели
(учтите, что 1800-й и 1900-й годы не были високосными) ?
Задача 15:
Назовем автобусный билет с шестизначным номером счастливым, если сумма цифр
его номера делится на 7. Могут ли два билета подряд быть счастливыми?
Задача 16:
Докажите, что из любых n целых чисел можно выбрать одно или несколько с
суммой, кратной.


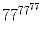 .
Задача 10:
Найдите две последние цифры числа а) 1999
.
Задача 10:
Найдите две последние цифры числа а) 1999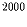 ;
б) 16
;
б) 16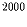 .
Задача 11:
Докажите, что Александр Юрьевич должен отпраздновать свое 28-летие в такой
же день недели, в какой он родился.
Задача 12:
В последовательности цифр каждая цифра, начиная с пятой, равна последней
цифре суммы четырех предыдущих. Последовательность начинается с цифр
1234096Может ли в ней встретиться комбинация цифр 1999?
.
Задача 11:
Докажите, что Александр Юрьевич должен отпраздновать свое 28-летие в такой
же день недели, в какой он родился.
Задача 12:
В последовательности цифр каждая цифра, начиная с пятой, равна последней
цифре суммы четырех предыдущих. Последовательность начинается с цифр
1234096Может ли в ней встретиться комбинация цифр 1999?